D-Wave neal(SA)の使い方

シミュレーテッドアニーリング(SA)とは

シミュレーテッドアニーリング（Simulated Annealing, 以下SA）は、「焼きなまし法」とも呼ばれ、最適化問題へのアプローチ方法の一つです。温度という概念を導入し、その温度をうまく制御することで解の探索をしています。この手法は統計力学における「高温で融解状態にある物質を徐々に冷却することで結晶状態に到達させるプロセス」に着想を得て、「温度を制御しながら初期解を徐々に改善して最適解に到達させるプロセス」を行なっています。

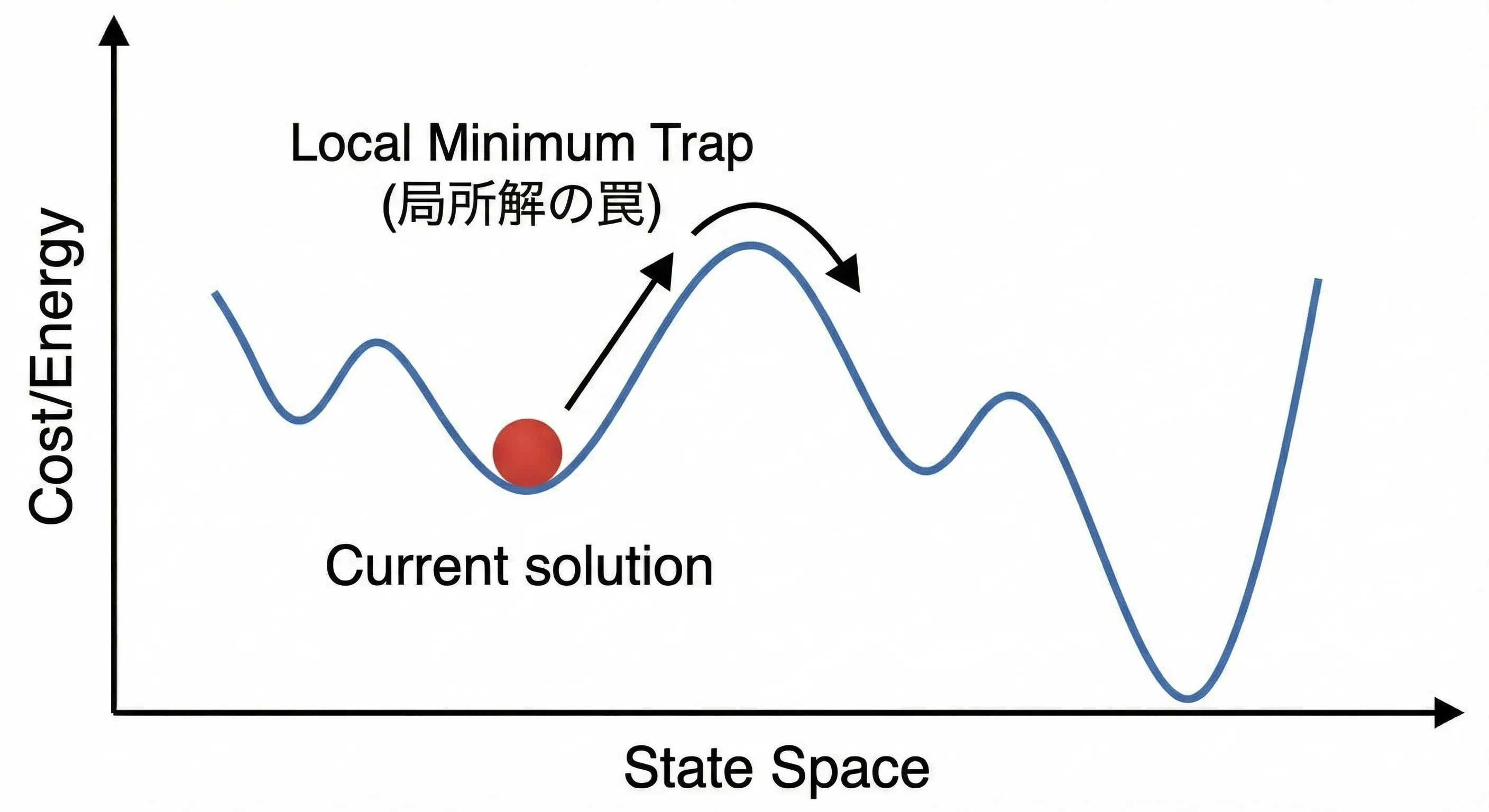
SAの模式図

SAのアルゴリズムの模式図を以下に示します。

横軸を状態空間、縦軸がエネルギーを示しています。赤い点が現在の解を示していて、一番小さい谷に落ちるように解を更新します。一方で、局所解のような抜けにくい谷がある場合、実際よりも高いエネルギーに落ちやすくなってしまう局所解の罠というものもあります。それを起こさないためにはゆっくりと温度を変化させるようにすると安定します。

アルゴリズム

SAの特徴として、エネルギーが悪化する方向の変更も一定の確率で許容しながら、最適解を探索するという特徴があります。アルゴリズムの流れは以下のようになります。

初期値をサンプリング
温度 $T$ を下げる
新たな点のサンプリング

$\Delta E= H(x')-H(x)$ を計算します。

ここで $H(x)$ はQUBOのエネルギー（目的関数値）です。

( $\Delta E < 0$ )：新しい解を採択（エネルギーが下がるため）。
( $\Delta E > 0$ )：確率 ( $P = \exp(-\Delta E / T)$ ) で採択（温度 $T$ が高いほど受け入れやすい）。

2~3を繰り返す

温度 $T$ を徐々に下げ、探索を収束させます。

この過程を多数回繰り返し、最終的に最小エネルギーの解を得ます。

Pythonによる実装例

ここからは、二次ナップサック問題をSAで解いた際のプログラムについて説明します。

ナップサック問題とは、価値と重さが定められた複数のアイテム中から、総重量の上限値がある中で，合計の利益が最大となるようにアイテムを選ぶ問題です。
アイテム $i$ を選ぶとき $x_{i}=1$ 、選ばないとき $x_{i}=0$ とします。また、アイテムの価値を $p_{i}$ 、重さを $w_{i}$ 、二次相互作用を $q_{ij}$ とします。

目的関数はこれらのパラメータを用いて以下のように書けます。

\begin{align*} f(x) &= \sum_{i=0}^{n-1} p_i x_i + \sum_{0 \le i < j \le n-1} q_{ij} x_i x_j \end{align*}

容量制約は

\begin{align*} \sum_{i=0}^{n-1} w_i x_i \le C \end{align*}

のように表せます。

したがって、最終的なコスト関数は

\begin{align*} E(x) &= -\sum_{i=0}^{n-1} p_i x_i - \sum_{0 \le i < j \le n-1} q_{ij} x_i x_j + \lambda \left( \sum_{i=0}^{n-1} w_i x_i - C \right)^2 \end{align*}

となります。

Step.0 ライブラリのインストール

Python では、D-Wave 社の dwave-neal というライブラリを使うことで SA を簡単に実行できます。

pipコマンドだけで簡単にインストールできます。

pip install dwave-neal

import neal

Step.1 問題データの定義

まず、二次ナップサック問題のデータを用意します。

アイテム数、利益、重さ、容量、二次相互作用の行列をそのままPythonの変数にします。

# アイテム数
n = 5

profits = [10, 8, 6, 4, 7]   # p_i
weights = [4, 3, 2, 1, 3]    # w_i
capacity = 7                 # C

# 二次相互作用 q_ij
Q_pair = [
    [0, 2, 0, 0, 1],
    [0, 0, 1, 0, 0],
    [0, 0, 0, 2, 0],
    [0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0],
]

Step.2 QUBO行列の作成

まず、元の目的関数部分をQUBO行列に入れます。

Q_qubo = {}

# 1. 元の目的関数部分（線形項）
for i in range(n):
    key = (i, i)
    Q_qubo[key] = Q_qubo.get(key, 0.0) - float(profits[i])

# 2. 元の目的関数部分（二次項）
for i in range(n):
    for j in range(i + 1, n):
        if Q_pair[i][j] != 0:
            key = (i, j)
            Q_qubo[key] = Q_qubo.get(key, 0.0) - float(Q_pair[i][j])

ここまでで「制約なし」の二次ナップサックが QUBOに変換できています。

次に、容量制約を守らせるために、罰金項をQUBO行列に追加します。

# 容量制約をどれくらい強く罰するかを決める係数
penalty = 10.0

# 3. 容量制約のペナルティの線形項
for i in range(n):
    lin_coeff = penalty * (weights[i] ** 2) - 2.0 * penalty * capacity * weights[i]
    key = (i, i)
    Q_qubo[key] = Q_qubo.get(key, 0.0) + lin_coeff

# 4. 容量制約のペナルティの二次項
for i in range(n):
    for j in range(i + 1, n):
        quad_coeff = 2.0 * penalty * weights[i] * weights[j]
        key = (i, j)
        Q_qubo[key] = Q_qubo.get(key, 0.0) + quad_coeff

これでQUBO行列の完成です。最後にSAで解いてみましょう。

Step.3 SAでQUBOを解く

dwave-nealのサンプラを使用します。

sampler = neal.SimulatedAnnealingSampler()

あとは用意したQUBO行列を送るだけです。

# QUBO を num_reads 回だけサンプリング
sampleset = sampler.sample_qubo(Q_qubo, num_reads=1000)

# 最良解（エネルギーが最小の解）を取り出す
best = sampleset.first
best_sample = best.sample
best_energy = best.energy

print("QUBOエネルギー:", best_energy)

Step.4 解を二次ナップサックの答えとして読み取る

どのアイテムを選んだか、総重さはいくつか、元の目的関数値はいくつか求めます。

# どのアイテムが選ばれたか（x_i = 1 の i）を取り出す
selected = [i for i in range(n) if best_sample.get(i, 0) == 1]

# 総重さ
total_weight = sum(weights[i] for i in selected)

# 元の目的関数の線形部分
lin_val = sum(profits[i] for i in selected)

# 元の目的関数の二次部分
quad_val = 0.0
for i in range(n):
    if best_sample.get(i, 0) == 0:
        continue
    for j in range(i + 1, n):
        if best_sample.get(j, 0) == 1:
            quad_val += Q_pair[i][j]

objective_value = lin_val + quad_val

print("選択されたアイテム:", selected)
print(f"総重さ: {total_weight} (容量 C = {capacity})")
print("目的関数の値:", objective_value)

if total_weight > capacity:
    print("※ 容量制約をオーバーしています。penalty を大きくしてください。")

実行結果

QUBOエネルギー: -512.0
選択されたアイテム: [0, 2, 3]
総重さ: 7 (容量 C = 7)
目的関数の値: 22.0

容量制約をオーバーせず、総価値を最大化できていることがわかります。

参考文献

[1] : dwave-neal Github, https://github.com/dwavesystems/dwave-neal, 閲覧日 2025/12/18