量子アニーリングにおける埋め込み

1. 量子アニーリングの概要

量子アニーリングでは、組合せ最適化問題を Ising モデルのエネルギー最小化問題として表します。

$$E = - \sum_i h_i \sigma_i^z \;-\; \sum_{(i,j) \in E} J_{ij}\, \sigma_i^z \sigma_j^z$$

ここで、$\sigma_i^z$ は量子ビットのスピン方向（$+1$ または $-1$）を表します。
このエネルギー関数を “ハミルトニアン” と呼びますが、ここでは 系のエネルギーを表す式 と考えていただければ十分です。

量子アニーリングでは、時間依存のハミルトニアン

$$H(t) = A(t)\left(-\sum_i \sigma_i^x\right) + B(t)\left(- \sum_i h_i \sigma_i^z - \sum_{(i,j)\in E} J_{ij}\sigma_i^z\sigma_j^z\right)$$

を徐々に変化させることで、エネルギー最小状態を探索します。
なお、第一項：$\sum \sigma^x_i$は組合せ最適化問題の解を重ね合わせた状態を作るために加える項であり、第二項は解きたい最小化問題を表します。

アニーリングの実行プロセス

アニーリングの初期状態では $A(t) \gg B(t)$ となっており、横磁場の効果が強い状態になります。このとき量子ビットは多くの候補状態を同時に探索することができます。そして時間の進行とともに横磁場を弱める一方で、問題のエネルギー関数に対応する項の重みである $B(t)$ を強めていくことで、系は徐々に最適化問題そのもののエネルギー構造に従うようになります。最終的には $A(t) \ll B(t)$ となり、問題を表す式のエネルギーが最小となる状態へと収束します。この状態が最適解に対応します。

	$A(t)$	$B(t)$	状態
アニーリング初期	大	小	横磁場が支配的で、量子ビットは多数の状態を同時に探索する重ね合わせ状態にある
アニーリング中盤	減少	増加	横磁場の影響が弱まり、問題のエネルギー構造に従うように誘導される
アニーリング終盤	小	大	問題ハミルトニアンが支配的となり、問題を表す式のエネルギーが最小となる

---

2. D-Wave の物理ビットとグラフ

量子コンピュータにおけるグラフとは

グラフとは、点（ノード）と線（エッジ）で構成されるネットワーク構造のことです。数学やコンピュータサイエンスでは、物事の関係性を表現するためによく使われます。

例えば、SNSで友人関係を表す場合、各人をノード、友人同士の繋がりをエッジで表現できます。

量子アニーリングマシンの物理構造を説明する際にもこの”グラフ”を使うことができて、以下のように対応づけることができます：

• ノード（頂点）：量子ビット（物理ビット）に対応します。各ノードは1つの量子ビットを表し、0または1の値（スピンでは+1または-1）を取ります。
• エッジ（辺）：量子ビット間の物理的な結合に対応します。エッジで繋がれた2つの量子ビット間には、二体相互作用 $J_{ij}$ を実装できます。

つまり、量子アニーリングマシンの物理グラフは、どの量子ビット同士が直接相互作用できるかを示しています。

Pegasus グラフ

D-Waveではソルバーによって採用されるグラフ構造が異なっていますが、 ここではD-Wave Advantageで採用されるPegasus グラフを例に説明します。

図1: Pegasusグラフ

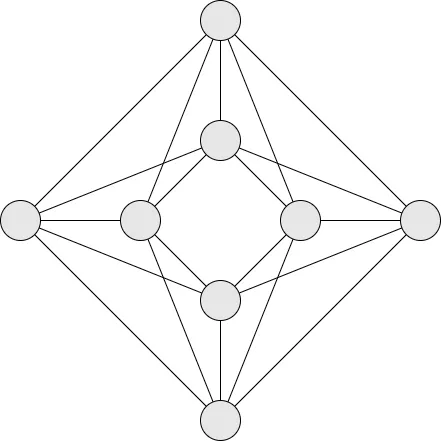
3. 量子アニーリングの埋め込み

量子アニーリングによって QUBO を解くには、このPegasus グラフ上に問題を適切にマッピングする必要があります。 例えば以下のQUBOの場合、物理グラフへのマッピングは以下のように実現できます。

$$H = x_1 x_2 + x_2 x_3 + x_3 x_4 + x_4 x_5 + x_5 x_1$$

図2: 埋め込み例

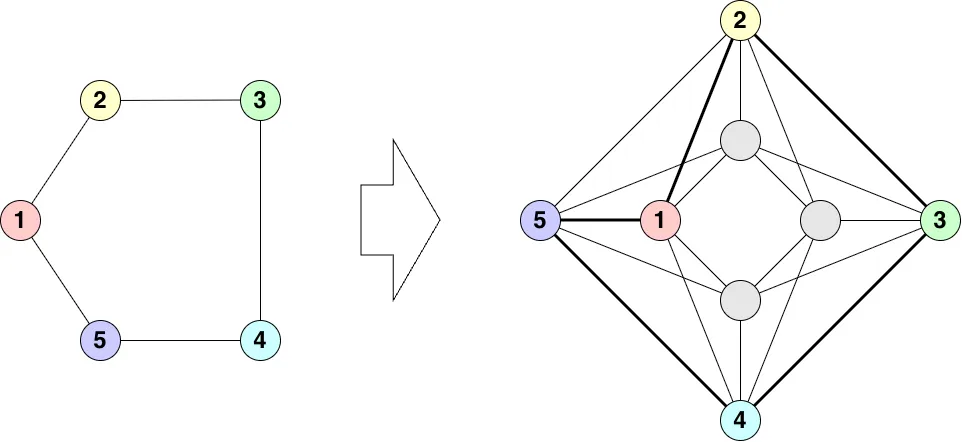
埋め込みの課題

しかしPegasus グラフにおいて接続できるノード数に限界があり、以下のようなQUBO 問題をそのままではマッピングすることができません。

$$H = \sum_{i=1}^5 \sum_{i<j}^5 x_i x_j$$

図3: 不可能な埋め込み例

---

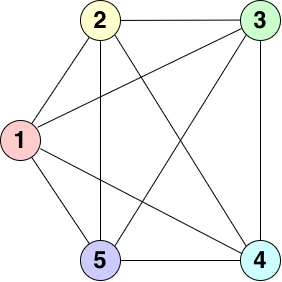
4. チェーンによる解決

複数の物理ノードに同一の論理ビットを割り当てることで、必要な結合を実現できます。このような同一ビットの物理ノードのグループを チェーン と呼びます。

図4: 埋め込み例(チェーンあり)

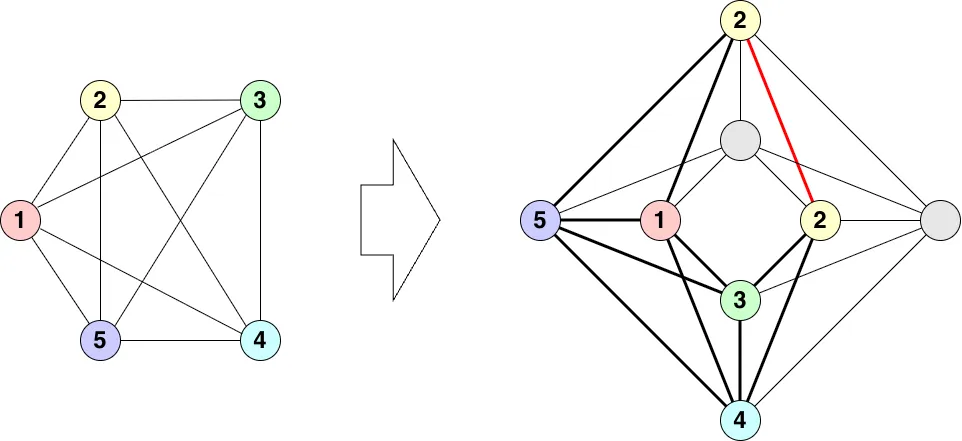
チェーンブレイクとチェーン強度

理想的には、同一チェーン内の全ての物理ビットが同じ値を取ることが期待されます。しかし実際のアニーリング実行結果では、チェーン内の物理ビットが異なる値を取ってしまう場合があります。この現象を チェーンブレイク(chainbreak) と呼びます。

そこでチェーン内の物理ビットが同一の値を保つようにするため、チェーン強度 を設定することで、チェーン内のビット間に強い負の相互作用を導入できます。ただしチェーン強度の調節によって埋め込みが変化するわけではなく、あくまでチェーン内部のエッジが相対的に強化されることに注意してください。

また、チェーン強度は高くし過ぎてしまうと本来解きたかった問題のエネルギーよりもチェーン維持のためのエネルギーが支配的になってしまい、結果的に最適解が得づらくなってしまう可能性があります。なので大きすぎず小さすぎない、適切な値に設定する必要があります。

---

5. D-Wave の物理グラフ構造の深掘り

D-Wave の量子アニーリングマシンでは、世代によって異なる物理グラフが採用されています：

• Pegasus グラフ：D-Wave Advantageで使用される物理グラフ構造
• Zephyr グラフ：D-Wave Advantage2 で使用される物理グラフ構造

図5: Zephyrグラフ

完全グラフの埋め込み

ではD-Wave の量子アニーリングマシンに埋め込める完全グラフの最大サイズ(=最大クリーク)はどれくらいでしょうか？どのようにチェーンを作成するかによっても変化しますが, 公式ドキュメントにより以下のように算出されます。

	マシン	最大クリーク
D-Wave Advantage	Pegasus	180
D-Wave Advantage2	Zephyr	172

ただし実施には欠損などによってこれよりも小さいサイズで限界となる場合もあるので目安として捉えてください。 また、この値は埋め込みが可能である最大のサイズを表しているだけで、量子アニーリングで効率的に解くことを保証するものではないことに注意が必要です。

Next-Generation Topologyの論文によるとPegasusグラフにおける最大クリークは$12(M-1)$であり, D-Wave AdvantageにおけるPegasusグラフのサイズパラメタは$M=16(P16)$であることから、D-Wave Advantageでの最大クリークは180と算出。

また、Zephyr Topologyの論文によるとZephyrグラフにおける最大クリークは$16M-8$であり, 公式ドキュメントによるとD-Wave Advantage2におけるZephyrグラフのサイズパラメタは$M=12(Z12)$であることから、D-Wave Advantage2での最大クリークは172と算出。

---

6. D-Wave での埋め込み実装

量子ビットへのマッピングは NP 完全問題であることが知られています。D-Wave SDK では minorminer と呼ばれるヒューリスティック手法を用いて、QUBO を自動的に物理グラフにマッピングし、アニーリングを実行します。

以下の実装例ではEmbeddingComposite によってD-Wave Advantage2ソルバーへの埋め込み処理を自動的に行って指定された QUBO 問題を解きます。また、使用するソルバーを変更することで、それに対応した物理グラフへ自動的に適切な埋め込みが行われます。

import os
from dwave.system import DWaveSampler, EmbeddingComposite

token = os.environ.get("DWAVE_API_TOKEN")
solver = "Advantage2_system1.7"

dwave_sampler = DWaveSampler(token=token, solver=solver)
sampler = EmbeddingComposite(dwave_sampler)

sampleset = sampler.sample_qubo(Q)