【中級者向け】計算複雑性とNP困難

前の章では「組合せ爆発」について触れました。要素数が少し増えるだけで、組合せ最適化問題の解の候補が天文学的な数字に膨れ上がり、それに伴って最適解を探すのにかかる時間も爆発的に増加していく現象です。これを計算複雑性理論の世界では 計算量 (Computational Complexity) という概念を用いて定量的に評価します。このページでは、問題の難しさを測るための基本的な考え方をもう少し詳しく説明します。

アルゴリズムの性能を評価する

問題の難しさ についての議論をするには、まずその問題を解くための アルゴリズムの性能 を議論しなくてはなりません。そこでまず、アルゴリズムの性能を評価するための基本的な考え方を理解しましょう。

計算量の増加の速さ

私たちがアルゴリズムの性能を評価する際、具体的な処理時間 (何秒かかるか) はあまり重要ではありません。それは使用するコンピュータの性能によって変わってしまうからです。重要なのは、「入力のサイズ $N$ が増えたとき、そのアルゴリズムの計算時間がどれくらい急速に増大するか」 です。

それでは、アルゴリズムの計算時間の増大の速さはどうやって理解すればよいでしょうか。1つの方法は、$N$ が非常に大きい値を取るときに計算時間がどれだけ増大するかを極限で計算する方法です。よく知られているように、次のことが成り立ちます。

$$\begin{aligned} \lim_{N \to \infty} \frac{2^N}{N!} &= 0, & \lim_{N \to \infty} \frac{N}{2^N} &= 0. \end{aligned}$$

つまり、$N$ がめちゃめちゃに大きくなっていくにつれて、

• べき乗 $N^a$ は平方根よりも速く発散し、
• 指数関数 $b^N$ は多項式よりも速く発散し、
• そして階乗 $N!$ は指数関数よりも速く発散する

ということがわかります。しかも、発散の速さは最も発散が速い項に影響を受けます。他にどんなに沢山項があっても、1つでも発散の速い項が存在すれば、式全体として発散が早くなるのです。そこで、アルゴリズムの計算量の増大の速さを評価する際には、もっとも発散の速い項にのみ着目します。

$$\begin{align*} & N \log N + 3N + \sqrt{N} &&\to && N \log N, \\ & 2^N + N^9 + N^3 &&\to && 2^N, \\ & 2N! + 2^N + 5 && \to && 2N!. \end{align*}$$

さらに、定数倍の違いはグラフの縦軸方向に伸び縮みする程度の変化でしかなく、グラフの曲線の形状そのものは変化ない ので、切り捨てて考えます。

$$\begin{align*} & 2N! &&\to &&N!, \\ & N \log 3 &&\to && N, \\ & a N \log N &&\to && N \log N. \end{align*}$$

指数よりも階乗のほうが発散が速いことは、次のスターリングの公式からわかる。

$$N! \simeq \sqrt{2 \pi N} \left(\frac{N}{e}\right)^N$$

ここで、$\simeq$ は $N \to \infty$ において両者が漸近することを意味する。

これが、計算量の増加の速さを測る基本的な考え方です。それでは、これを数学的にもう少ししっかり定義する方法を考えましょう。

ランダウのビッグオー記法

先ほどの「指数関数は多項式より速く、階乗は指数関数より速く発散する」という主張は、次のように言い表すことができます。

ノート

主張

どんな $a>0, b>1$ に対しても、ある十分大きな実数 $N_0$ よりも大きな自然数 $N$ に対しては

• 指数関数 $b^N$ は多項式 $N^a$ よりも大きくなり
• 階乗 $N!$ は指数関数 $b^N$ よりも大きくなる

といえる。

これは次のように書くこともできます。

$$\forall a > 0, \forall b > 1, \exists N_0 \in \mathbb R \text{ s.t. } \forall N \in \mathbb{N}, N > N_0 \implies N^a < b^N < N!$$

このような計算時間の増え方を表すのに、ランダウのビッグオー記法 を使うと便利です。

ノート

定義

ある関数 $f(n)$ と $g(n)$ があって、これらは自然数に対して非負の実数値を返す関数とする。

$$f, g: \mathbb{N} \to \mathbb{R}_{\ge 0}$$

このとき、$f(n) = O(g(n))$ であるとは、以下の条件が成り立つことをいう。

$$\exists c > 0, \exists n_0 > 0 \, \text{s.t.} \, \forall n \in \N, n \ge n_0 \implies f(n) \le c \cdot g(n)$$

つまり、$f(n) = O(g(n))$ であるとは、入力サイズ $n$ がある地点 $n_0$ を超えれば、あとはどんなに $n$ が増えても $f(n)$ は常に $c \cdot g(n)$ 以下に収まる (上から抑えられる) という意味です。

この記号を使うと、先ほどの「最も発散が速い項のみに注目する」という部分は、次のように表すことができます。

$$\begin{align*} & 2N! &&= &&O(N!), \\ & N \log 3 &&= &&O(N), \\ & a N \log N &&= &&O(N \log N). \end{align*}$$

さて、ビッグオー記法の定義によれば、実は以下のようなことも言えます。

$$\begin{align*} & 2N! &&= &&O(N!), \\ & 2^N &&= &&O(N!), \\ & a N \log N &&= &&O(N!). \end{align*}$$

具体的に考えてみよう

$2^N = O(N!)$ ということはできますが、逆に $N! = O(2^N)$ ということはできません。$2^N$ を何倍したとしても、$N$ が十分大きければ、$2^N$ よりも $N!$ のほうが大きくなっていってしまうのです。これを具体的に見てみましょう。たとえば、$f(N) = 10^{100} \times 2^N$、$g(N) = N!$ とします。そうすると、$N$ が比較的小さいうちは

$N$	$f(N)$	$g(N)$	大小関係
$10$	$= 1.024 \times 10^{103}$	$= 3.6288 \times 10^6$	$f(N) \gg g(N)$
$11$	$= 2.048 \times 10^{103}$	$= 3.99168 \times 10^7$	$f(N) \gg g(N)$
$12$	$= 4.096 \times 10^{103}$	$= 4.790016 \times 10^8$	$f(N) \gg g(N)$

と、確かに圧倒的に $g(N)$ のほうが大きいです。ところが、この関係はほどなく逆転します。

$N$	$f(N)$	$g(N)$	大小関係
$81$	$\approx 2.42 \times 10^{124}$	$\approx 5.79 \times 10^{120}$	$f(N) \gg g(N)$
$82$	$\approx 4.84 \times 10^{124}$	$\approx 4.75 \times 10^{122}$	$f(N) \gg g(N)$
$83$	$\approx 9.67 \times 10^{124}$	$\approx 3.95 \times 10^{124}$	$f(N) > g(N)$
$84$	$\approx 1.93 \times 10^{125}$	$\approx 3.31 \times 10^{126}$	$f(N) < g(N)$
$85$	$\approx 3.87 \times 10^{125}$	$\approx 2.82 \times 10^{128}$	$f(N) \ll g(N)$

これ以降は常に $f(N) < g(N)$ が成り立ちます。

以上は単に $c=10^{100}$ の例を取ってきただけですが、これに限らず、どんなに $c$ を大きく設定したとしても、$N!$ はいつか必ず $c \times 2^N$ を追い越してしまいます。そういうわけで、$N! = O(2^N)$ は成り立ちません。

ちなみに

ランダウの記号 $O(f(N))$ は単に $N\to\infty$ における漸近挙動を記述するのみならず、より一般に $x$ が何らかの値に収束していく際の漸近挙動を記述するのにも使われます。たとえば、指数関数のマクローリン展開

$$\exp( a x ) = \sum_{k=0}^\infty \frac{(a x)^k}{k!} = 1 + ax + \frac{(ax)^2}{2!} + \frac{(ax)^3}{3!} + \cdots (x \approx 0)$$

を2次の項で打ち切って、3次以降の項を無視するという操作は

$$\exp( a x ) = 1 + ax + \frac{a^2}{2} x^2 + O(x^3) \quad (x \to 0)$$

などと表すことができます。この場合のランダウの記号の定義は次のように表すことができます。

ノート

定義

実数値を受け取り、実数値を返す関数

$$f, g: \mathbb{R} \to \mathbb{R}$$

に対して $f(x) = O(g(x)) \, (x \to a)$ であるとは、以下の条件が成り立つことをいう。

$$\exists C > 0, \exists \delta > 0 \, \text{s.t.} \, \forall x, 0 \lt |x - a| \lt \delta \implies |f(x)| \le C \cdot |g(x)|$$

なお $x \to a$ という部分は、誤解のない限りよく省略されることが多いです。

問題の難しさを評価する

ここまでで、

• アルゴリズムの性能指標の1つは、$N$ が増加したときにアルゴリズムの計算時間がどれくらい増えるかに注目することである
• $N$ が十分に大きいときには、最も大きな項に注目すればよい
• 最も大きな項の増加の速さを表すにはビッグオー記法を使う

ということがわかりました。このことを活用することで、問題の「難しさ」について、定量的な議論ができるようになります。

最悪計算量の定義

「問題 $Q$ は難しい」と一言で言っても、その意味は曖昧です。「どんな入力に対しても難しいのか？」「どんな解き方でも難しいのか？」という問題が生じてくるのです。

そこで、以下の順序で「最悪なケース」の難しさを定義していきます。

1. 入力サイズを固定する。 議論の土台として、入力データの長さ (サイズ) を一律で $N$ とします。

2. 「ある解法」で「ある具体例」を解く時間を考える。 ある問題 $Q$ (例：ナップサック問題全体) に含まれる、特定の具体例 $I$ (例：荷物が5個の場合の特定の数値設定) を考えます。 この具体例 $I$ を、ある特定のアルゴリズム $A$ で解くときにかかる計算時間を $T_A(I)$ とします。

3. 最悪ケースを考える (Worst-case)。 次に、アルゴリズム $A$ の性能を評価します。 問題 $Q$ には無数の具体例 $I_1, I_2, \dots$ が含まれますが、その中で 最も計算に時間がかかる具体例 (最悪ケース) を解くときの時間を、そのアルゴリズムの計算量 $T_A(Q)$ とします。

   $$T_A(Q) = \max_{I \in Q} T_A(I)$$

   つまり、運が悪くても、このアルゴリズムなら最大でこれくらいの時間で解ける という保証をするわけです。

4. 最良のアルゴリズムを選ぶ。 最後に、問題 $Q$ そのものの難しさを定義します。 問題 $Q$ を解くことができるアルゴリズムは $A_1, A_2, \dots$ と無数に考えられます。その中で、「最も高速な (効率的な) アルゴリズム」 を用いたときの計算時間を、問題 $Q$ の時間計算量 $T(Q)$ とします。

   $$T(Q) = \min_{A \in \mathcal{A}(Q)} T_A(Q)$$

少し複雑になったので、用語を表で整理しましょう。

記号	意味	内容の例
$N$	入力データの長さ
$Q$	問題のクラス	「線形計画問題」「ナップサック問題」など
$I$	問題の具体例	$Q$ に含まれる特定の数値設定のインスタンス
$A$	アルゴリズム	「内点法」「動的計画法」など
$T_A(I)$	具体的な計算時間	具体例 $I$ をアルゴリズム $A$ で解く時間
$T_A(Q)$	アルゴリズムの性能	$Q$ のうち 最も難しい 具体例を $A$ で解く時間 (最悪計算量)
$T(Q)$	難しさ (最悪計算量)	最も高速な $A$ を選んだときの $T_A(Q)$

以上をまとめると、問題 $Q$ の難しさ $T(Q)$ は、次のように定義することができます。

ノート

定義

• $Q$: 問題のクラス
• $\mathcal{A}(Q)$: その問題を解くことができるアルゴリズムの集合
• $T_A(I)$: アルゴリズム $A$ で具体例 $I$ を解くときの計算量

とする。問題 $Q$ の最悪計算量 $T(Q)$ を次式で定義する。

$$T(Q) = \min_{A \in \mathcal{A}(Q)} \left( \max_{I \in Q} T_A(I) \right)$$

つまり 「最悪ケースの具体例を解くのにかかる時間が最も短いアルゴリズムを選んだときの、その計算時間」 を、問題 $Q$ の難しさ $T(Q)$ と定義するということです。

私たちが「$N$ が大きくなるにつれてどれほど計算時間が長くなるのか」に興味があるとき、この $T(Q)$ をオーダー記法を用いて $T(Q) = O(f(N))$ と表し、「問題 $Q$ の難しさは $O(f(N))$ である」と言います。

注意: この定義が意味すること

1. 「確実に解けるアルゴリズム (厳密解法) 」のみを対象とする。 ここでのアルゴリズム $A$ は、常に正しい最適解を出力することが保証されている必要があります。 メタヒューリスティクス (遺伝的アルゴリズムやシミュレーテッドアニーリングなど) は、短時間で「最適解に近い解」を出せるかもしれませんが、それが本当に最適解である保証がないため、ここでの「問題の難しさ」の定義におけるアルゴリズム $A$ には通常含まれません。

2. 「最悪ケース」について論じている。 ここで定義した「難しさ」は、あくまで「最も時間がかかる意地悪なインスタンス」に対するものです。 逆に言えば、「理論上は非常に難しい (NP困難である) 」とされる問題でも、「実用上現れるデータの範囲ではそれほど難しくない」 というケースは多々あります。 また、最悪ケースでは指数時間かかるとされていても、平均的なデータに対しては多項式時間で解けることが知られている問題もあります。

クラスPとクラスNP

ここまで「計算量」という指標で問題の難しさを定義してきました。この指標を使うことで、クラスPとクラスNPという2つの問題の難しさを定義することができます。

決定問題

通常、最適化問題は「最小のコストを求めよ」という形式ですが、複雑性の理論ではこれを 「コストが $K$ 以下になる解は存在するか？ (Yes / No) 」 という形式に変換して考えます。この問題と最適化問題の関係は後で説明しますが、ここではとりあえず、「決定問題は最適化問題を Yes / No で答える形式に変更したバージョンだ」という程度で理解すればOKです。

この決定問題に対して、「最悪計算量」と「実際に解けるかどうか」という2つの観点から、以下の2つのクラスが定義されます。

クラスP (Polynomial)

クラスP に属する問題は、「多項式時間で解を見つけることができる決定問題」 です。いわゆる「効率的に解ける」問題はこのクラスに含まれると考えて良いでしょう。

ノート

定義

決定問題 $Q$ がクラスPに属するとは、ある決定性チューリングマシンと多項式 $p(N)$ が存在し、任意の入力サイズ $N$ のインスタンスに対して、$p(N)$ 時間以内で正しい Yes / No の答えを出力できることをいう。

決定性チューリングマシンはいわゆる「普通のコンピュータ」のことを指しています。

クラスNP (Nondeterministic Polynomial)

多くのパズルには、「答えを見つけるのは難しいが、答えが合っているか検算 (判定) するのは簡単である」 というある種の非対称性があります。

ヒント

例 (数独)

数独は

• 空欄をすべて埋めるのは大変だが
• 「埋められた数字がルールに違反していないかチェックする」のは一瞬

である。

この性質に着目したのが クラスNP です。

ノート

定義

決定問題 $Q$ がクラスNPに属するとは、Yesとなる任意のインスタンス $I$ に対して、ある 証拠 (Witness) または 証明 (Certificate) $W$ が存在し、その $W$ を用いることで、多項式時間で「答えがYesであること」を検証できることをいう。

簡単に言えば、 「もし『これが正解だ』という証拠をくれたら、その証拠を元に、本当にYesであるかどうかを多項式時間で判定 (検算) できる問題」 がクラスNPに相当します。

ヒント

例 (巡回セールスマン問題の決定問題バージョン版)

「コスト $K$ 以下で回るルートはあるか？」という問いに対して、自力でルートを見つけるのは大変。しかし、もし誰かが「このルートなら $K$ 以下だ」と具体的なルート (証拠) を提示してくれれば、距離を足し算するだけで本当に $K$ 以下か、すぐに (多項式時間で) 確認できる。

注意: NPは “Not Polynomial” (多項式時間ではない＝難しい) の略ではありません。正しくは “Nondeterministic Polynomial” (非決定性多項式時間) の略です。

クラスNPという名前は、「非決定性チューリングマシン (Nondeterministic Turing Machine)」(並列世界ですべての可能性を同時に試せるような仮想的なウルトラスーパーハイスペックな並列マシンのようなもの) を用いて多項式時間で解ける、という定義に基づいています。

問題の難しさの比較について

ここからは、問題同士の「相対的な難しさ」を比較する方法を考えていきましょう。そのための1つの方法は、「一方の問題がもう一方の問題の答えを教えてくれるかどうか」 です。

多項式時間還元

ある問題 $A$ を解く手続きの中で、別の問題 $B$ を解く手続きを利用できるとします。このとき、「もし問題 $B$ を解くアルゴリズム (サブルーチン) があれば、それを使って問題 $A$ も多項式時間で解ける」ならば、問題 $B$ は問題 $A$ 以上の難しさを持つと言えます。

これを厳密に定義するために、オラクル (神託) という概念を使います。オラクルとは、ある問題の入力を与えると、瞬時に (1ステップで) 正しい解を返してくれる仮想的なブラックボックスのことです。

ノート

定義

サブルーチンである問題 $B$ を解くための仮想的なオラクルを $\mathcal{O}_B$ とする。問題 $A$ を解くアルゴリズム $\mathcal{M}$ が存在し、その $\mathcal{M}$ が以下の条件を満たすとき、問題 $A$ は問題 $B$ に 多項式時間還元可能 であるといい、$A \leq_p B$ と表記する。

1. (構成可能性) アルゴリズム $\mathcal{M}$ は、実行中に $\mathcal{O}_B$ を何度でも呼び出すことで、任意の問題 $A$ の入力に対して正しい解を出力する。
2. (計算効率性) $\mathcal{O}_B$ の呼び出しを1ステップと数えた場合、アルゴリズム $\mathcal{M}$ 全体の計算時間は、入力サイズ $N$ の多項式時間以内である。

この定義が意味することは以下の2点です。

1. 「もし問題 $B$ を多項式時間で解ける (実在のプログラムが存在する) ならば、それをサブルーチンとして使うこのアルゴリズム $\mathcal{M}$ によって、問題 $A$ も多項式時間で解ける」
2. (対偶) 「もし問題 $A$ が多項式時間で解けないほど難しいならば、サブルーチンとして使われている問題 $B$ もまた (多項式時間では) 解けないほど難しい」

そういうわけで、これが成り立つ時、直感的には「問題 $B$ の難易度は問題 $A$ 以上である」と言えます。不等号

$$A \leq_p B$$

は、問題の難しさの大きさを抽象的に表していると理解すればよいです。

NP困難 (NP-Hard) と NP完全問題 (NP-Complete)

還元の概念を使うことで、クラスNPに関連する「最も難しい」問題群を定義できます。

NP困難 (NP-Hard)

NP困難とは、「NPに属するすべての問題以上に (少なくとも同等に) 難しい問題」のことです。

ノート

定義：NP困難

問題 $H$ が NP困難 (NP-Hard) であるとは、任意の NP に属する問題 $L$ が、$H$ に多項式時間還元可能であることをいう。

$$\forall L \in \text{NP}, \quad L \leq_p H$$

なお、NP困難な問題 $H$ 自身は、NPに属している必要はありません。NPよりもはるかに難しいクラス (判定すら多項式時間でできない問題など) に属していても構いません。

NP完全問題 (NP-Complete)

NP困難 (任意のNP問題よりも難しい) 問題で、かつ 自分自身はNP (検算は簡単) である ような決定問題を「NP完全問題」と呼びます。

ノート

定義：NP完全問題

問題 $C$ が NP完全問題 (NP-Complete) であるとは、以下の2条件を満たすことをいう。

1. $C \in \text{NP}$ ($C$ 自身が NP に属する)
2. $C$ は NP困難である (すべての NP 問題から還元可能)

注意: この定義に従えば、NP完全問題は決定問題でなくてはいけないので、「ある最適化問題はNP完全問題である」という表現は適切ではないと言えます。用語の使い方には注意しましょう。。。

ヒント

具体例: 巡回セールスマン問題 (TSP) とその決定問題バージョンは以下のようにクラスが異なる。

• 例「コスト $K$ 以下で全都市を回るルートは存在するか？ (Yes/No)」はNP完全問題である。

  • この問題はすべてのNP問題から多項式時間還元可能である。
  • かつ、もし「これがルートだ」と証拠を渡されれば、$K$ 以下かどうかの判定 (検算) は多項式時間でできるため、NPに属する。

• 例「全都市を回る最小コストのルートとそのコスト自体を求めよ」はNP困難である。

  • 上記の問題はこの問題に多項式時間還元可能なので (なぜなら、この問題が解ければ上記の問題にも即座に答えられるから) 、任意のNP問題はこの問題に多項式時間還元可能である。
  • しかし、これは決定問題ではないので、NPには属さない。

クラスPとクラスNPの関係

「NP完全問題」という「NPの中で最も難しい問題」が定義できたことで、クラスPとクラスNPの関係についてより深く議論することができます。

P は NP の部分集合

定義から明らかなように、クラスPに含まれる問題は、すべてクラスNPに含まれます ($\rm P \subseteq NP$)。 なぜなら、自力で多項式時間で「解ける」問題は、当然ながら多項式時間で「検算」もできる (自分で解いて答え合わせすればよい) からです。

P vs NP問題

では、その逆、つまり 「検算が簡単な問題は、すべて解くのも簡単なのか？ ($\rm P \stackrel{?}{=} NP$)」 という問いはどうでしょうか。実は、この問いは現代の計算機科学における最大の未解決問題の一つである 「$\rm P \neq NP$ 予想」 と呼ばれる問題です。この問題については、現時点では証明も反証もされていません (少なくとも、証明されることも反証されることも非常に難しいことだけはわかっています) 。

ヒント

例えば、証明することを考えてみましょう。$\rm P=NP$ を証明する1つの方法は、NP完全問題を多項式時間で解くアルゴリズムを探すことです。先ほど定義した NP完全問題 の性質を思い出しましょう。

NP完全問題 $C$ は、すべてのNP問題 $L$ から多項式時間還元可能 ($L \leq_p C$)。

これは、「もし、たった1つでもNP完全問題を多項式時間で解くアルゴリズムが見つかれば、その還元を使って、すべてのNP問題を多項式時間で解けるようになる (つまり P=NP となる) 」 ということを意味します。しかし、現時点でそのようなアルゴリズムは1つも見つかっていません。

逆に、$\rm P \neq NP$ を証明するには、NP完全問題が原理的に多項式時間で解けないことを示せばよいのですが、これは単に1つアルゴリズムを発見するよりも圧倒的に難しそうです。

以上は素朴な見方ですが、歴史的には $\rm P \neq NP$ 予想に決着をつけるために考案された様々な手法が、その方法では原理的に証明も反証も不可能であることが後から証明される という泥沼の様相が繰り広げられてきました。

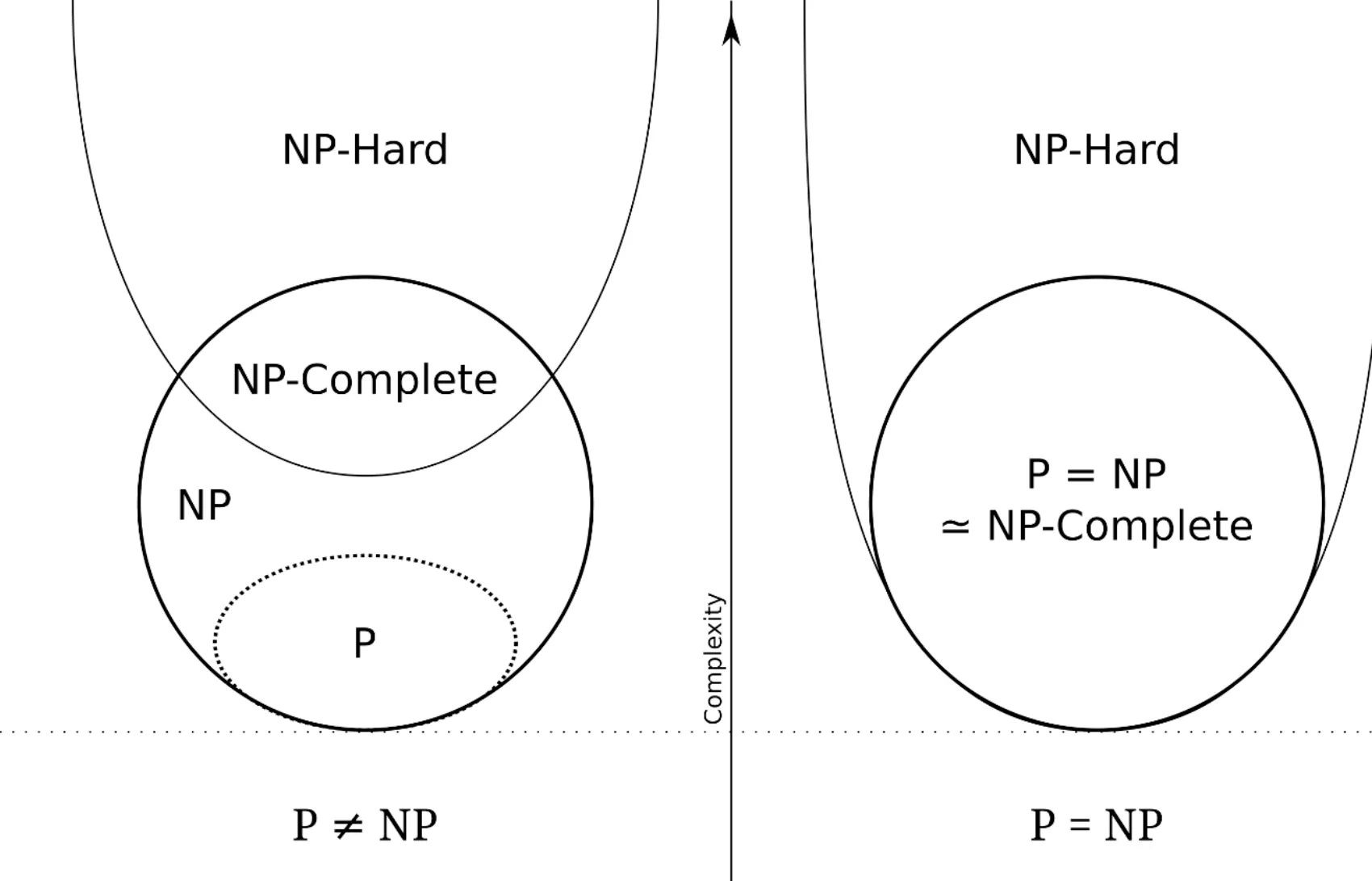Euler diagram for P, NP, NP-Complete, and NP-Hard set of problems. Licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic and 1.0 Generic license. Attibution: Behnam Esfahbod

現在では、NP完全な問題は数千個程度見つかっているにも関わらず、どの1つに対しても多項式時間で解けるようなアルゴリズムが見つかっていないことから、多くの研究者は $\rm P \neq NP$ (検算は簡単だが解くのは難しい問題は、実際に存在する) と予想しています。

厳密解を諦める

さて、私たちが産業応用で直面する組合せ最適化問題の多くは 「NP困難」 に属します。これが意味することは重大です。

$\rm P \neq NP$ と予想される現在、NP困難な問題の厳密解 (数学的保証のある正解) を多項式時間で求めるアルゴリズムは存在せず、少なくとも問題の大きさ $N$ に対して指数関数的に計算時間がかかることとなります。そのため実用的な方法で問題を解くには「完璧さ」を諦め、アプローチを抜本的に変える必要があります。

最悪計算量の定義の箇所でも少し触れたように、ここまでの話は最悪な場合の計算量を考慮する話でした。つまり最も困難なケースを考慮する話であり、平均的にはそこまでめちゃめちゃな計算時間の増え方をするとも限りません。そこで、発想を転換して、

• 平均的な問題インスタンスについては、ほぼ厳密解に近い正解を与える。
• 稀に現れる最悪なインスタンスについては、それなりに。

というものを目指します。

近似解法とヒューリスティクス

このようなアプローチは、得られる解の数学的厳密さに着目すると大きく2つに分類されます。

• 近似解法:
  • 理論上の最適解から一定以内の近さの解を求める。
  • 得られた解は「厳密解からの近さ」が保証される (解のコスト間数値は厳密解のコスト関数値の◯◯%以下であるなど)。
• ヒューリスティクス:
  • 経験的に (統計的に) 良い解が得られることがわかっている方法を使う。

量子アニーリング (QA) やシミュレ―テッドアニーリング (SA) などは、ヒューリスティクスとして扱われます。つまり、数学的に厳密ではなく、またどれほど正しい解を与えてくれるかの確実な保証も不十分だが、平均的な問題に対してはかなり良い答えをくれるものとして理解されています。

それでは、実際問題としてQAやSAはどれほど良いのか? もっと厳密解に近づけるにはどうすればよいのか? そのような問いが、現在の研究の中心課題となっています。