組合せ最適化問題
この章では、最適化問題の中でも特に組合せ最適化問題について学びます。
1. 組合せ最適化問題とは？
Section titled “1. 組合せ最適化問題とは？”組合せ最適化問題とは、前章に説明した離散最適化問題の中でも特に組合せ的な構造から最適解を探索する問題です。 ザックリ言うと、組合せの中から “最も良い組合せ” を見つける問題です。
代表的な組合せ最適化問題
Section titled “代表的な組合せ最適化問題”以下に、代表的な組合せ最適化問題をまとめます。
-
巡回セールスマン問題
都市集合を一筆書きで巡回し、総移動距離が最短となる経路を求める問題。 -
最大カット問題
グラフの頂点集合を2つの部分に分割し、境界となる辺の重み（または本数）を最大化する問題。 -
ナップサック問題
重量制約のもとで、価値の合計が最大となる品物の組合せを選択する問題。 -
グラフ彩色問題
隣接する頂点が同じ色にならないように彩色し、必要な色数（彩色数）を最小化する問題。
2. 組合せ最適化問題の難しさ
Section titled “2. 組合せ最適化問題の難しさ”組合せ最適化問題の多くは、計算量理論の観点から 計算量的に困難なクラス に分類されます。
直感的には、「候補となる組合せの数があまりにも多く、1つ1つ試していては到底間に合わない」タイプの問題です。
ここでは、組合せ最適化問題の難しさの中でも、特に解の候補数が指数関数的に増えてしまう 「組合せ爆発」 に由来する側面に焦点を当てます。
組合せ問題最適化問題の難しさについて理解するため、下の図のようなの正方形の格子上を左下のスタートから右上のゴールに進むことを考えます。 しかし、進み方には制限があり、上か右にだけ進むことができるものとします。この時、スタートからゴールまでの経路はいくつあるでしょうか？
図に示した程度の大きさであれば（頑張れば）数え上げることもできますし、高校数学で習う重複を含む順列として考えると簡単に計算することができます。
今回の場合は、↑つ、→つを1列に並べたものがいくつあるか数えることに対応するので以下のように通りと計算することが出来ます。
これは前章で述べた変数の取り得る値・状態数の数と見ることも出来ます。
組合せを「最適化」する
Section titled “組合せを「最適化」する”先ほど述べた組合せを最適化するとはどういうことでしょうか？
次の例として、先ほどの正方形の格子に二重丸のポイントを加えた下の図のような状況を考えます。
進み方は先ほどと同じだとした場合に、ポイントを最大化 することが出来る経路はどれでしょう？
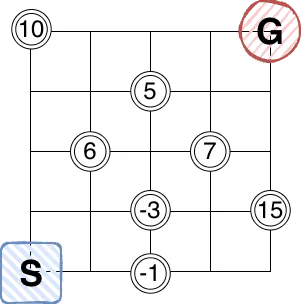
これも実際に経路をたどって試してみると、例えば右に回、上に回行った点が最も稼げると分かります。 今回のように所々にポイントがある場合なら目で見ても分かりそうですが、全ての格子点上にポイントがあったり、正のポイントと負のポイントがバラバラに配置されていたりしたらどうでしょう？ ポイントを最大化 することが出来る経路を見つけることは大変に思えてきませんか？
組合せの増え方
Section titled “組合せの増え方”「通りくらいなら頑張ってしらみ潰しにたどれるよ！」という人もいるかもしれません。
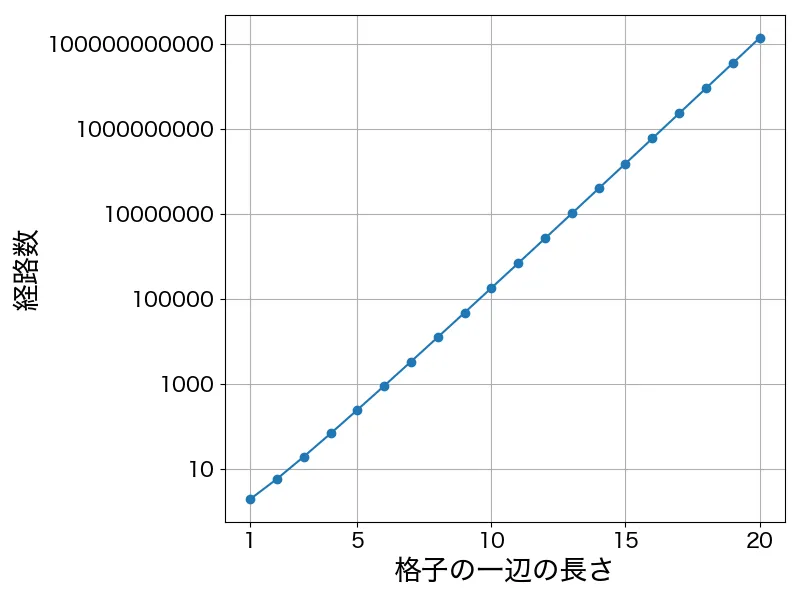
では、さらに大きい格子を考えるとどうでしょうか？一辺の長さを変えた時の経路数を片対数プロットしたものが下の図になります。 長さがになるだけで経路数はと膨大な数になります。ここまでくると人間には明らかに難しそうですし、コンピュータを使っても計算時間がかかりすぎてしまう大きさになります。これが組合せ最適化問題の難しさにつながる 「組合せ爆発」 になります。
3. 組合せ最適化問題の解法
Section titled “3. 組合せ最適化問題の解法”では、どうやってこのような組合せ最適化問題を解くのでしょうか？
方針は大きく分けて2つあります。
- 最適解（厳密解）を求める方法
- 近似解・良さそうな解を求める方法
問題のサイズや求められる精度によって、どちらの方針をとるかが変わります。
最適解（厳密解）を求める方法
Section titled “最適解（厳密解）を求める方法”1つ目は、最適解を保証付きで探す アルゴリズムを用いる方法です。
組合せ爆発を抑え込みながら、賢く全探索していくイメージです。
代表的な手法としては次のようなものがあります。
-
全探索（Brute Force）
力技で全ての組合せを試す方法です。 小さな問題に対しては、すべての組合せを試して最適解を見つけることもできますが、問題サイズが大きくなるとすぐに現実的ではなくなります。 -
動的計画法（Dynamic Programming; DP）
問題を部分問題に分解し、部分問題の計算結果を利用することで効率的に解く方法です。
格子上の経路数を数える問題や、ナップサック問題などで広く登場します。 -
分枝限定法（Branch and Bound）
探索木を分割（分枝）しつつ、「これ以上探索しても最適解を上回ることはない」と判断できた部分木を切り落としていく（限定）ことで、実質的な探索量を削減する方法です。 多くの組合せ最適化ソルバーの基盤になっています。
こうした手法の長所は、「最適解であることが保証される」点です。
一方で 大規模な問題では計算時間やメモリが膨大になる ため、現実的には解けないことも多くなります。
近似解・ヒューリスティクスで解く方法
Section titled “近似解・ヒューリスティクスで解く方法”2つ目の方針は、最適解にはこだわらず、そこそこ良い解(近似解)を現実的な時間で見つける 方法です。 大規模な組合せ最適化問題では、こちらが実務上の主役になることも多いです。
-
貪欲法（Greedy Algorithm）
「その時点で一番よさそうな選択」を順番に積み重ねていくシンプルな方法です。
計算は速い一方で、必ずしも全体として最適な解になるとは限りません。 -
近似アルゴリズム（Approximation Algorithms）
一部の問題では、「最適解の近似率○%以内」という性能保証付きのアルゴリズムが知られています。理論的な保証と実用性のバランスを取るアプローチです。 -
メタヒューリスティクス（Metaheuristics）
局所探索を賢く制御して、局所解からの脱出や探索の多様性を確保する枠組みです。
代表例として以下のような手法があります。- シミュレーテッドアニーリング（Simulated Annealing; SA）
- 遺伝的アルゴリズム（Genetic Algorithm; GA）
- タブーサーチ（Tabu Search） など
-
量子アニーリング（Quantum Annealing; QA）
組合せ最適化問題をイジングモデルなどにマッピングし、
量子効果を利用して低エネルギー状態（＝良い解）を探索する手法です。
このドキュメントで紹介されるシミュレーテッドアニーリングや量子アニーリングは、
いずれも「最適解の保証よりも、現実的な時間で良い解を得ること」を重視した手法に分類されます。
厳密解法と近似解法の使い分け
Section titled “厳密解法と近似解法の使い分け”-
問題規模が小さい / 最適解がどうしても必要
→ 分枝限定法・動的計画法・整数計画ソルバなど、厳密解法を使う。 -
問題規模が大きい / 制限時間内で「そこそこ良い解」が欲しい
→ 貪欲法・局所探索・メタヒューリスティクス・量子アニーリングなど、
近似解法・ヒューリスティクスを使う。
このドキュメントでは、特に後者のシミュレーテッドアニーリング や 量子アニーリング などに焦点を当てていきます。
アルゴリズムの詳細については、他の章に委ねます。