最適化問題とは何か

この章では、最適化問題について紹介します。

1. 最適化問題とは

最適化問題とは

ある目的関数を最も”良い”値とするために、
制約条件を満たしながら変数をどのように選べばよいかを決める問題

です。
例として、目的関数が小さければ小さいほど”良い”、最小化問題を考えてみます。数式を用いると上記の内容は、以下のように書き換えることが出来ます。

\begin{align*} &\text{最小化}\ \ \ f(\vec{x}) \\ &\text{制約条件}\ \ \ \vec{x}\in\mathcal{X}． \end{align*}

$f(x)$ ：目的関数
$\mathcal{X}$ ：実行可能集合（制約条件を満たす変数 $\vec{x}$ の集合）
$\vec{x}$ ：変数

目的関数 $f(x)$ を最小にする入力 $\vec{x}$ のことを 最適解 と呼びます。
目的関数を最小化するのではなく、最大化する場合も同様に最適化問題です。 $f(x)$ を最小化する問題というのは、 $-f(x)$ を最大化すると対応するので、同じ問題として扱うことができます(※同じ制約条件の下で)。

制約条件 $x \in \mathcal{X}$ とは、変数 $x$ が取り得る値です。例えば、 $-1 \leq x \leq 1$ のような不等式制約を満たす $x$ のみ取ることが出来るなどが挙げられます。他にも、実数全体 $x \in \mathbb{R}$ を取ることが出来る、 $x \in \{0, 1\}$ のように離散値のみを取ることが出来るなども制約条件です。

変数 $x$ として、連続値を扱う問題を連続最適化問題、離散値(整数値、ブール値)を扱う問題を離散最適化問題(組合せ最適化問題) と呼びます。

2. 最適化問題の種類

最適化問題と一口に言っても、先ほど登場した、連続最適化問題、離散最適化問題(組合せ最適化問題)　をはじめとして、目的関数の形や変数の種類、制約条件の有無によってさまざまな分類があります。
ここでは、実務や研究でよく登場する代表的な最適化問題について紹介します。最適化問題においては、 「変数が連続値か、離散値か」 が最適解を探索する際の手法・アルゴリズムの選択において重要な違いとなります。

連続最適化問題

前述したように変数 $x$ が実数をとる最適化問題です。実社会問題として登場する場面の例としては以下が挙げられます。

例：
- 機械学習のパラメータ最適化
- 物理シミュレーションのエネルギー最小化
- 企業の生産量の最適化

連続最適化問題の特徴としては、微分が使えるため、最適解を探索する際に解析的手法や勾配降下法などが利用しやすい点にあります。

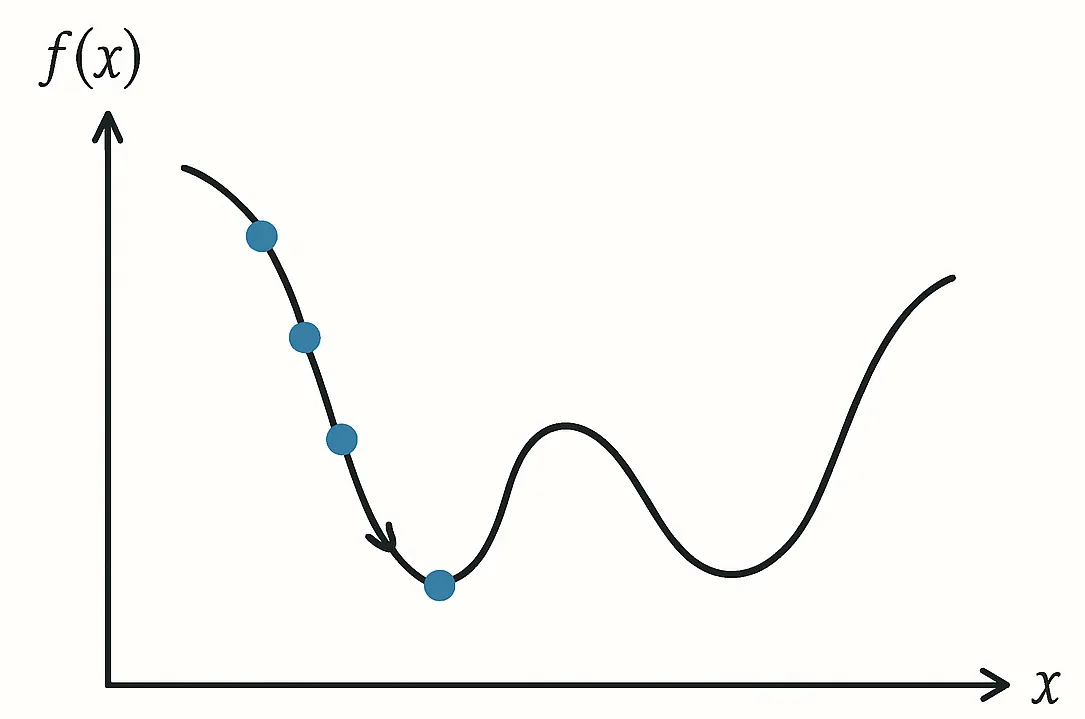
連続最適化問題の目的関数 $f(x)$ は、形状として以下の図のような(基本的には)なだらかな形状としてイメージすることができます。勾配から目的関数が小さくなる方向を事前に知ることが出来ます。その方向に徐々に谷を下っていくことで目的関数の最適解もしくは、局所解を探索することが出来ます。連続最適化問題の目的関数

離散最適化(組合せ最適化)

変数が $x$ が 整数値 や 0/1（ブール値） をとる場合です。実社会問題として登場する場面の例としては以下が挙げられます。

例：
- ナップサック問題（入れる・入れないの2択）
- スケジューリング（割当・順序の最適化）

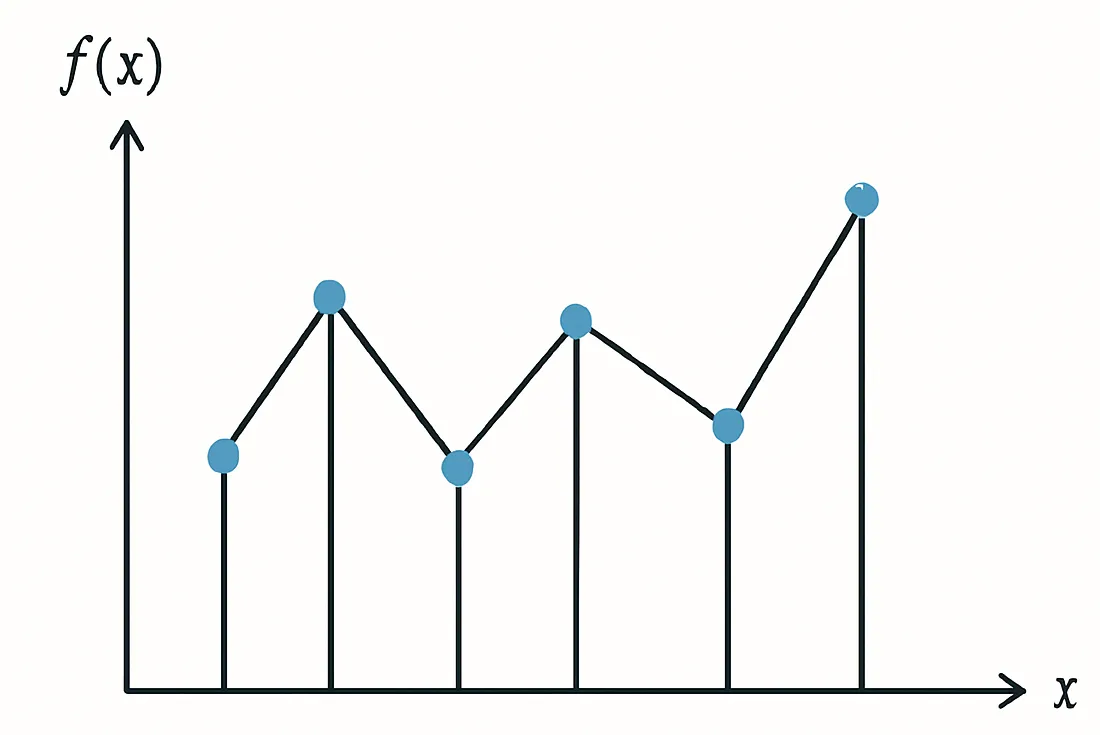
連続最適化問題の特徴としては、連続最適化のように勾配を考慮することが一般には出来ません。また、組合せ爆発(以降のセクションで説明)が起こる為、全探索することが現実的ではない場合が多いです。離散最適化問題の目的関数 $f(x)$ は、以下のような形状であるとイメージできます。離散最適化問題の場合には、勾配から目的関数が小さくなる方向を事前に知ることができない為、実際に移動し、その変数に対して目的関数を評価することになります。離散最適化問題の目的関数

組合せ最適化とQUBO

特に量子アニーリングの文脈では、離散最適化(組合せ最適化)のうち QUBO（Quadratic Unconstrained Binary Optimization） と呼ばれる問題について扱います。

変数は $x_{i} \in \{0, 1\}$ の二値変数
目的関数は二次形式(二次関数) $\sum_{ij} Q_{ij}x_{i}x_{j}$
制約を全てペナルティとして目的関数に組み込む（＝制約なし問題として解く）
- 仮にペナルティを破ってしまった場合に、目的関数の値が上昇するようにペナルティを設計することで、制約を満たさない解が選ばれないようにします。

巡回セールスマン問題、スケジューリング・クラスタリングなど、多くの組合せ最適化問題がQUBOに書き換えることが出来ますこれらの定式化手法については、Ising formulations of many NP problems, Andrew Lucas(2014)に詳しく記載されています。

3. 最適化問題を定式化してみる

以下では、実際の身近な例を「最適化問題」として定式化してみます。数学・英語・国語の3科目に対して、合計30時間の勉強時間をどう配分すれば 合計点が最大になるか という離散最適化問題を考えます。

各科目に割り当てる時間を以下のように変数と、勉強時間を1時間単位で区切る設定とします。

数学： $t_{\text{math}} \in \mathbb{Z}_{\geq 0}$
英語： $t_{\text{eng}} \in \mathbb{Z}_{\geq 0}$
国語： $t_{\text{jpn}} \in \mathbb{Z}_{\geq 0}$

ここで、 $\mathbb{Z}_{\geq 0}$ とは0以上の整数を表す記号です。

目的関数（合計点）

現実には、どれだけ勉強すればどれほどの点数をとれるかは分からないので、今回各科目の点数は「得点効率 × 1時間」で与えられると仮定した問題を考えることにします。各科目の 点数効率（点／1時間） を次のように設定します。

数学： $20$
英語： $10$
国語： $5$

このとき、合計点（目的関数）は

f(t_{\text{math}}, t_{\text{eng}}, t_{\text{jpn}}) = 20\, t_{\text{math}}+ 10\, t_{\text{eng}}+ 5\, t_{\text{jpn}}

となります。

制約条件

合計点(目的関数)を最大化することを目指しますが、現実的にはある制約条件を満たしながら最適化問題を解く必要があります。今回考慮する制約について整理します。

総勉強時間は30時間以内：

時間は有限ですので、限られた時間で合計点(目的関数)を最大化することを目指します。

t_{\text{math}} + t_{\text{eng}} + t_{\text{jpn}} \le 30

各科目60点以上必要：

合計点(目的関数)を最大化することを目指しますが、各科目で合格点(60点)以上を取るべきです。

\begin{aligned} 20\, t_{\text{math}} &\ge 60,\\ 10\, t_{\text{eng}} &\ge 60,\\ 5\, t_{\text{jpn}} &\ge 60, \end{aligned}

各科目は最大100点：

各科目で取ることが出来る点数は100点以下です。

\begin{align*} 20\, t_{\text{math}} &\le 100,\\ 10\, t_{\text{eng}} &\le 100,\\ 5\, t_{\text{jpn}} &\le 100, \end{align*}

これらの条件を各変数 $t_{\text{math}}, \, t_{\text{eng}}, \, t_{\text{jpn}}$ の制約条件に書き換えると以下のようになります。

3\le t_{\text{math}} \le 5,\\ 6\le t_{\text{eng}} \le 10,\\ 12\le t_{\text{jpn}} \le 20.

定式化のまとめ

以上より、この問題は次の最適化問題 として定式化することが出来ました。

\begin{align*} \text{最大化}\ \ \ \ \ &20\, t_{\text{math}}+ 10\, t_{\text{eng}}+ 5\, t_{\text{jpn}} \\ \text{制約条件}\ \ \ \ \ &t_{\text{math}} + t_{\text{eng}} + t_{\text{jpn}} \le 30\\ & 3\le t_{\text{math}} \le 5,\\ & 6\le t_{\text{eng}} \le 10,\\ & 12\le t_{\text{jpn}} \le 20 \\ & t_{\text{math}}, \, t_{\text{eng}}, \, t_{\text{jpn}} \in \mathbb{Z}_{\geq 0} \end{align*}

最適解を求める

結論から記載すると、この最適化問題の最適解は以下です。

※点数効率の高い数学、英語、国語の順に貪欲に時間を割り当てることで最適解を発見することが出来ます。

t_{\text{math}}^* = 5,\\ t_{\text{eng}}^* = 10,\\ t_{\text{jpn}}^* = 15

この時の合計点数(目的関数)は以下のように $275$ 点と計算できます。

f(t_{\text{math}}^{*}, t_{\text{eng}}^{*}, t_{\text{jpn}}^{*}) = 20\, t_{\text{math}}^{*}+ 10\, t_{\text{eng}}^{*}+ 5\, t_{\text{jpn}}^{*} = 100 + 100 + 75 = 275

4. 最適化アルゴリズムについて

今回定式化を行なった最適化問題は、人が考えた直感的な方法（貪欲法）によって最適解を簡単に見つけることができました。しかし、一般的な最適化問題では、目的関数の形状が複雑であったり、制約条件が多岐にわたることがあるため、直感的なアプローチだけで最適解を求めることは困難です。特に、離散最適化問題では、探索空間の大きさが指数関数的に増大する 「組合せ爆発」 (次の章で説明)が起こるため、全ての解を調べる全探索は現実的ではありません。

そのため、最適解や良い近似解を効率的に求めるための最適化アルゴリズムが非常に重要となります。他のページで説明されている量子アニーリングも最適化アルゴリズムの一種です。最適化アルゴリズムは問題の構造（連続・離散、制約の種類、目的関数の性質など）に応じて適切に選択する必要があります。

次の章では、特に離散最適化問題（組合せ最適化問題）に焦点を当て、なぜ解くことが難しいのか、そしてどのようなアルゴリズムや考え方が用いられているのかを説明していきます。