量子アニーリングで解くための問題定式化

1. 最適化問題の基礎

1.1 量子アニーリングとは

膨大な組み合わせの中から最適解を求める組合せ最適化問題を、近似的に高速に解くことが期待されている手法の一つに量子アニーリング（Quantum Annealing） があります。
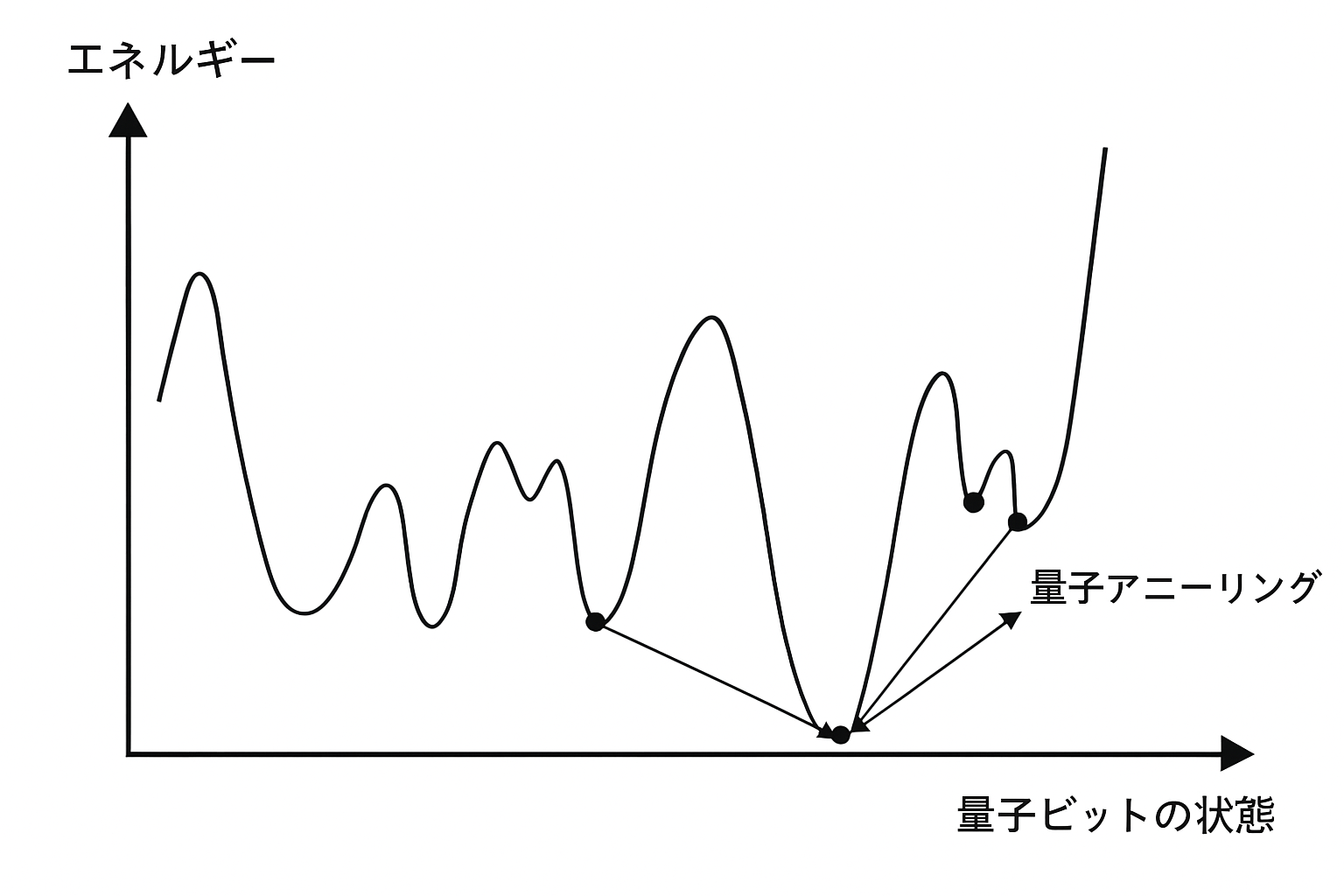
量子アニーリングでは、解くべき問題を“エネルギーがどれだけ高いか” を表す関数 $E(x)$ として表現します。そして、物理法則に従ってこのエネルギーが最も低くなる状態（谷底）を自然に探し出す仕組みになっています。
高校数学で学ぶ二次関数

y = a(x - b)^2

を思い出してみてください。このグラフは下に凸で、一番低い点＝最小値（頂点）が明確です。
量子アニーリングは、この谷底を探す操作を、もっと複雑な問題に拡張した技術となっています。

1.2 定式化とは

では、量子アニーリングに問題を渡せばすぐ解いてくれるのでしょうか？
残念ながら そのままでは何もできません。
人間にとっては次の

「A と B のどちらかを選ぶ」
「作業 C は 14 時以降に行う」
「予算 10 万円以内」

といった記述は直感的に解釈できますが、コンピュータにとってはただの文字列です。
そこで重要なのが、“問題を解きやすい形に整えること＝定式化” です。
定式化では、現実の問題から次の 3 つを整理する必要があります。

どんな選択肢を表すか → 変数を決める
何を良くしたいか → 目的関数を決める
何が許されるか → 制約を決める

1.3 変数の種類とその扱い

最適化問題を数学で表すとき、まず「どのような変数を使うか」を決めます。
実は変数には様々な種類があります：

連続変数（例：0〜100 のどれか）
整数変数（例：人数、台数など）
二値変数（0 か 1 だけ。選ぶ／選ばない）

代表的なものをいくつか挙げましたが、どれも最適化問題では重要な役割を果たします。では、量子アニーリングで問題を解く時にはどの変数を使うべきなのでしょうか？

実は量子アニーリングで扱うことができるのは「0/1 の二値変数」だけなのです。

量子アニーリングにおける情報の基本単位である 量子ビット(qubit) は、物理的に 0 の状態 または 1 の状態をとります。つまり、ハードウェアそのものが 0/1 で世界を表現する設計になっている のです。そのため、問題を量子アニーリングに渡すためには、すべての選択肢を

x_i \in \{0,1\}

という 二値の世界に翻訳する必要があります。 一見ただの数字ですが、見方を変えると「選ぶか？選ばないか？」という選択肢のように見ることもできます。多くの組合せ最適化問題はこのように2つの選択肢で表すことができます。

その作業を割り当てる → 1 / 割り当てない → 0
そのルートを使う → 1 / 使わない → 0

そのため、二値変数は 現実の選択の構造と相性がよい です。

1.4 目的関数と制約条件

一般的な最適化問題の定式化において、扱う変数を決めた後に必要になるのが目的関数 と 制約条件 です。目的関数とは、 「何を良くしたいのか」 を数値で表した式のことです。

ここでは有名なナップサック問題を例にして考えてみます。 $N$ 個の品物があるとします。品物 $i$ をナップサックに入れるなら $x_i=1$ 、入れなければ $0$ と定義します。そして、各品物にはそれぞれ価値が $v_i$ と決められています。この時、価値を最大にしたい時は価値の合計の最大化 を考えれればいいことになります。これを数式で表すと以下のようになります。

\max \sum_{i=1}^N v_i x_i

なお、先ほど量子アニーリングは最小化解を見つける手法だと紹介しました。実は最小化と最大化は数学的には同じ形式で扱えます。
最大化したいときは、目的関数にマイナスをつければ「小さくする＝最小化問題」と同じ扱いになります。

\max f(x) \;\Longrightarrow\; \min [-f(x)]

ですので、先ほどの最大化したい数式は以下のような最小化問題で表すことができます。

\max \sum_{i=1}^N v_i x_i = \min \left( - \sum_{i=1}^N v_i x_i \right)

さて、ナップサック問題の目的関数だけを考えると、すべての商品を詰め込むことで価値の合計が最大になるという当然の結果が得られてしまいます。しかし、実際にはナップサックの容量には限りがあるため、追加の条件を考える必要があります。
このような条件を数学的に表現したものを 制約条件 と呼びます。制約条件とは、解が 「満たすべきルール」 を数式として示したものです。

例えば、品物1、品物2、品物3のうち、２つまでしかナップサックに入れることができないという制約がある場合は以下のような等式を満たせばいいことになります。

x_1+x_2+x_3 = 2

また、別の制約条件として例えば、品物1と品物2を同時に入れてはいけない場合は、次のようになります。

x_1 x_2 = 0

このように、二値変数を使うと、「足し算」と「掛け算」だけでこれらを表現できることが大きな利点です。