Application to Scheduling Problems (Part 1)

Note

This article introduces the Workforce Scheduling Problem (WSP) as a practical application of optimization using QUBO formulation.

1. Background

1.1 What is the Workforce Scheduling Problem (WSP)?

A workforce scheduling problem (WSP) aims to improve productivity, level out workloads, and optimizing labor costs by assigning the right worker with the right skills to the right task at the right time, using information of workers, tasks and a schedule. In practical applications, WSP is widely used to efficiently allocate limited personnel in areas such as at factory lines, call centers, hospitals or nursing homes, and rotation management in logistics warehouses.

Difficulties

Common challenges of WSP include:

• As the number of workers and tasks increases, the assignment process itself becomes complex.

• Finding an optimal assignment for large-scale problems requires significant computational time.

• Real-world requirements have a lot of constraints and therefore make it difficult to find an exact solution.

Typical Objectives

Optimization goals for scheduling often include:

• Minimizing the total number of employees required.
• Balancing workloads across the team.
• Minimizing the makespan (the total time to complete all tasks).

In this article, we aim to determine an assignment that minimizes the overall schedule (the makespan) while considering task sequences and individual workloads, as illustrated in Table 1. Table 1 is called a Gantt chart, which illustrates a project schedule, and is often used to manage software design in the software industry and work flow and personnel in the manufacturing industry.

Table 1: Personnel assignment visualization (Gantt chart)

Project Name	Task	Person-months	Aug. Week 1	Aug. Week 2	Aug. Week 3	Aug. Week 4
Project A	Task 1	0.1	Worker A
Project A	Task 2	0.2	Worker A
Project A	Task 3	0.25		Worker A
Project A	Task 4	0.5			Worker A	Worker A
Project B	Task 1	0.25	Worker B
Project B	Task 2	0.1		Worker B
Project B	Task 3	0.15		Worker B

1.2 What is Person-Months?

In project management, work volume is often measured in person-hours or person-months. A person-month represents the amount of work one person can complete in one month.

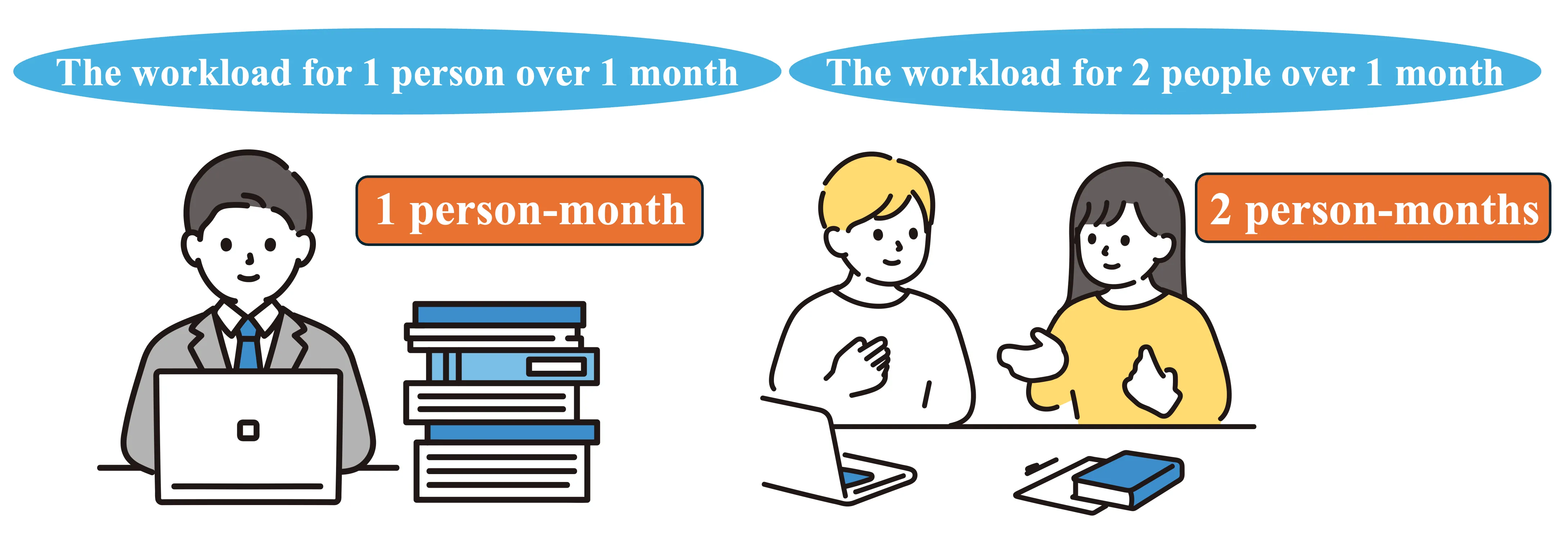
In other words, $\text{Person-months}=\text{Number of workers} \times \text{Duration (Months)}.$

---

2. Optimization Conditions

This time, we will formulate this WSP using the Quadratic Unconstrained Binary Optimization (QUBO) format by considering the following conditions:

1. Minimize the makespan.

2. Consider how efficiently different workers complete specific tasks.

3. Ensure workers are only assigned to tasks that they are qualified for.

4. Respect requested time slots for specific tasks.

5. Maintain the required order of tasks within a project.

To generate a valid Gantt chart, we also add the following constraints:

1. Task continuity

2. Workload limits in order to prevent over-assigning a single worker

2.1 Key points in this formulation

While many WSP models with QUBO formulation exist, this formulation specifically addresses:

• Different workers have different skills - task effort changes based on the assigned worker’s proficiency.

• Each task has a time window when a task must or should be started.

• Rigid dependencies between some tasks are already determined.

3. Mathematical Formulation

Here we will show how to formulate the conditions introduced in the previous section.

We represent the WSP as an energy function $E$. The goal is to find the configuration of variables that minimizes this value:

$$E = \alpha E_\alpha + \lambda_1 E_1 + \lambda_2 E_2 + \lambda_3 E_3 + \lambda_4 E_4 + \lambda_5 E_5,$$

where $\alpha$ and $\lambda (i=1,\,2,\,3,\,4,\,5)$ are the weights (hyperparameters) of each term. $E_\alpha$ represents the objective term, and $E_i(i=1,\,2,\,3,\,4,\,5)$ are the following constraint terms.

The first term $E_\alpha$ represents the total makespan. This problem aims to minimize this term.

$$E_\alpha = \sum_{p} \sum_{f} \sum_{t} t\, x_{p,f,t}.$$

The second term $E_1$ ensures that the schedule meets person-months requirements while considering different skills of different workers:

$${E_1 = \sum_{f} \qty( \sum_{p} \sum_{t} d_{p,f}\, x_{p,f,t} - \frac{20}{d_{t}} A_{f} )^{2}}.$$

The third term $E_2$ is designed to guarantee task continuity:

$${E_2 = \sum_{p} \sum_{f} \sum_{t} \qty( x_{p,f,t} - x_{p,f,(t+1)} )^{2}}.$$

The fourth term $E_3$ is a constraint that prohibits assigning multiple tasks at the same time to one resource:

$${E_3 = \sum_{p} \sum_{t} \qty( \sum_{f} x_{p,f,t} - \frac{1}{2} )^{2}}.$$

The fifth term $E_4$ ensures that tasks are not assigned during restricted periods:

$$E_4 = \sum_{f} \sum_{t} \sum_{p} (1 - D_{f,t})\, x_{p,f,t}.$$

The sixth term $E_5$ handles precedence constraints, ensuring tasks are executed in the specific order defined within each project:

$${E_5 = \sum_{(i \prec j)} \sum_{t} \qty( \sum_{p} x_{p,j,t} ) \qty( \sum_{p'} \sum_{t' \ge t} x_{p',i, t'} )}.$$

Detailed explanations of each term can be found in Application to Scheduling Problems (Part 2).

Note

This is just one example; we encourage you to experiment with your own decision variables $x$ and formulations.

Keep It Simple.

Avoid adding unnecessary terms. A complex formulation can make it impossible to satisfy all constraints simultaneously and may exceed the qubit capacity of current annealing hardware.

3.1 Setting Decision Variables

The first step in formulation is defining the decision variables. For this problem, we define $x_{p,f,t}$ as follows:

$$x_{p,f,t} = \begin{cases} 1 \colon & \text{Worker $p$ handles task $f$ at time unit $t$}. \\ 0 \colon & \text{Otherwise}. \end{cases}$$

Tip

Adding more indices to the decision variable allows for broader interpretations of what $x$ represents.

Note

However, be aware that this can make results harder to interpret or increase the number of qubits required, potentially exceeding the capacity of current quantum hardware for large-scale problems.

3.2 Setting Constants

Defining the constants used in the formulation is a crucial part of the process. For this example, we set the following constants in Table 2.

Table 2: Constants definition

Constant	Description	Possible values
$d_t$	The minimum allocation unit (fixed at 0.1 for this experiment)	Positive real number
$d_{p,f}$	Workload multiplier when worker $p$ handles task $f$	Non-neg real number
$A_f$	Estimated person-months for task $f$	Positive real number
$D_{f,t}$	Whether task $f$ is scheduled to occur in week $t$	0 (False) or 1 (True)

In this scenario, we assume a workday of 7.5 hours. Here, the minimum allocation unit indicates the time unit for task allocation. $d_t = 0.1$ means that tasks are allocated in units of 1/10 of a day (0.75 hour or 45 minute).

3.3 Setting Hyperparameters

We define the hyperparameters (weights) that adjust the strength of each term:

• $\alpha \in \mathbb{R}$ (real number): Weight for the objective term.
• $\lambda_1,\lambda_2,\lambda_3,\lambda_4,\lambda_5\in \mathbb{R}$ (real number): Weight for the individual QUBO constraints.

Tip

Tuning these hyperparameters is critical. By balancing the order of magnitude for each term, you can find the better weights more easily. Aim for a simple formulation because tuning becomes harder as terms increase.

---

4. Summary

Using the Gantt charts common in software development and manufacturing as an example, this page introduced how to treat personnel scheduling as an optimization problem, from conceptual phase to mathematical formulation. Mathematically formulating an optimization problem requires distinguishing between fixed constants and decision variables. Correctly identifying these roles is the first step toward an accurate solution. There are many ways to formulate optimization problems. We encourage you to explore references and other articles to find the setting that best fits your specific real-world problem.

For more details on this formulation, specific constant values, and the obtained scheduling results, please refer to the sequel: Application to Scheduling Problems (Part 2).

This research is currently being prepared for publication. Details are subject to change.

---

5. References

• Serap Ulusam Seçkiner and Mustafa Kurt. “A simulated annealing approach to the solution of job rotation scheduling problems,” Applied Mathematics and Computation 188.1 (2007), 31-45
• Tadashi Kadowaki and Hidetoshi Nishimori, “Quantum annealing in the transverse Ising model,” Physical Review E 58.5 (1998), 5355

---

6. Writer

Second-year master’s student in the Ohzeki group at Graduate School of Information Sciences, Tohoku University

Kaito Yashiro

(Translated by Ami Koshikawa)