スケジューリング問題への応用（後編）

ノート

最適化問題の応用例として、スケジューリング問題の紹介をします。なお、このページではスケジューリング問題への応用（前編）の定式化から詳しく解説していきます。

1. この記事の概要（前回のおさらい）

このページでは、スケジューリング問題への応用（前編）で紹介した定式化について、 その詳細な説明や具体的な定数の設定方法、そして、最適化を実行した結果までを順を追って解説します。

前編では、人員スケジューリング問題において最適化のために考慮すべき条件をいくつか挙げました。それらの条件をもとに、以下のような定式化を紹介しました。

$$E = \alpha E_\alpha + \lambda_1 E_1 + \lambda_2 E_2 + \lambda_3 E_3 + \lambda_4 E_4 + \lambda_5 E_5$$

それでは、定式化の意味と各項の詳しい内容を見ていきましょう。

---

2. 定式化の解説

ここではスケジューリング問題への応用（前編）の定式化を詳しく解説していきます。

2.1 何をしているのか

スケジューリング最適化のための目的関数として メイクスパン（全体の終了時刻）を最小化する項 を設定し、そこに必要な各種の制約条件を加えることで問題を定式化しています。

具体的には、次のような観点を制約として数式に組み込んでいます。

• 実際に担当した作業量が、見積もり工数を満たしているかどうか
• タスクが適切に連続して割り当てられているか（不自然な途切れがないか）
• 1人の作業者が同時に複数のタスクを担当しないようにする（マルチタスク禁止）
• 作業者やタスクごとに「この日程に割り当てたい」という希望を反映する
• プロジェクトごとに定められたタスク順序が守られているかどうか

これらの制約を組み合わせることで、実際の現場に近い形でスケジューリングを最適化できるようになります。

2.2 各項の説明と理解

以下では、定式化のそれぞれの項について詳しく解説していきます。

第1項について

第1項はMakespan（スケジューリング全体の期間）の最小化をするための目的項です。

$$E_\alpha = \sum_{p}\sum_{f}\sum_{t} t\, x_{p,f,t}.$$

より遅い期間にタスクを割り当てるほど、項全体の値が大きくなるように設計しています。 つまり、QUBOソルバーによって、より短い期間でタスクを終わらせる効果を図る項になっています。

第2項について

第2項は各作業者の作業工数の変化を考慮しながら、実際に割り当てたタスクが見積もり工数を満たすように制約を設ける項です。

$$E_1 = \sum_{f}\left(\sum_{p}\sum_{t} d_{p,f}\,x_{p,f,t} - \frac{20}{d_{t}} A_{f}\right)^{2}.$$

それぞれの作業者$p$が担当したタスク$f$を合計し、その値に各作業者のタスクごとの工数変化である実質作業倍率$d_{p,f}$をかけることで工数を数え上げるようになっています。 その値が、人月を人日に直した$20A_{f}$と等しくなるように設計しています（1ヶ月あたりの作業日を20日と定義しています）。 なお、今回は日付の最小単位を$t$と定義しているため、左辺と単位を合わせるために$d_t=0.1$で割っています。

第3項について

第3項は割り当てるタスクの連続性を保証するために設計した制約項です。

$$E_2 = \sum_{p}\sum_{f}\sum_{t}\!\left(x_{p,f,t} - x_{p,f,(t+1)}\right)^{2}.$$

ある作業者$p$がタスク$f$を時間$t$担当した際には、時間$t+1$にも同じタスクをしてもらうという意味を持ちます。 各作業者$p$を時間の最小単位$t$に割り当てる際に、この項がなければ、連続してタスクを行うことを考慮できなくなります。 具体的には、終わらせるのに3時間必要なタスクがあった際に、9:00 〜 12:00にタスクを割り当てるのが理想ですが、 9:00 〜 10:00、14:00 〜 15:00、16:00 〜 17:00に割り当てられるというような効率の悪い割り当て方を防ぐ役割があります。

第4項について

第4項は同時刻に複数のタスクを割り当てることを禁止する制約項です。

$$E_3 = \sum_{p}\sum_{t}\!\left(\sum_{f} x_{p,f,t} - \frac{1}{2}\right)^{2} .$$

ある作業者$p$のある時間$t$に注目した際に、そのタスク$f$の合計が1つまたは割り当てないことを意味しています。この式において、$1/2$ではなく1を使うと、必ずその時間に1つのタスクを割り当てなければならないという強い制約になりますが、メイクスパン最小化の項と衝突してうまく割り当てが行われないことがあるため、$1/2$を選択しています。

1/2制約について

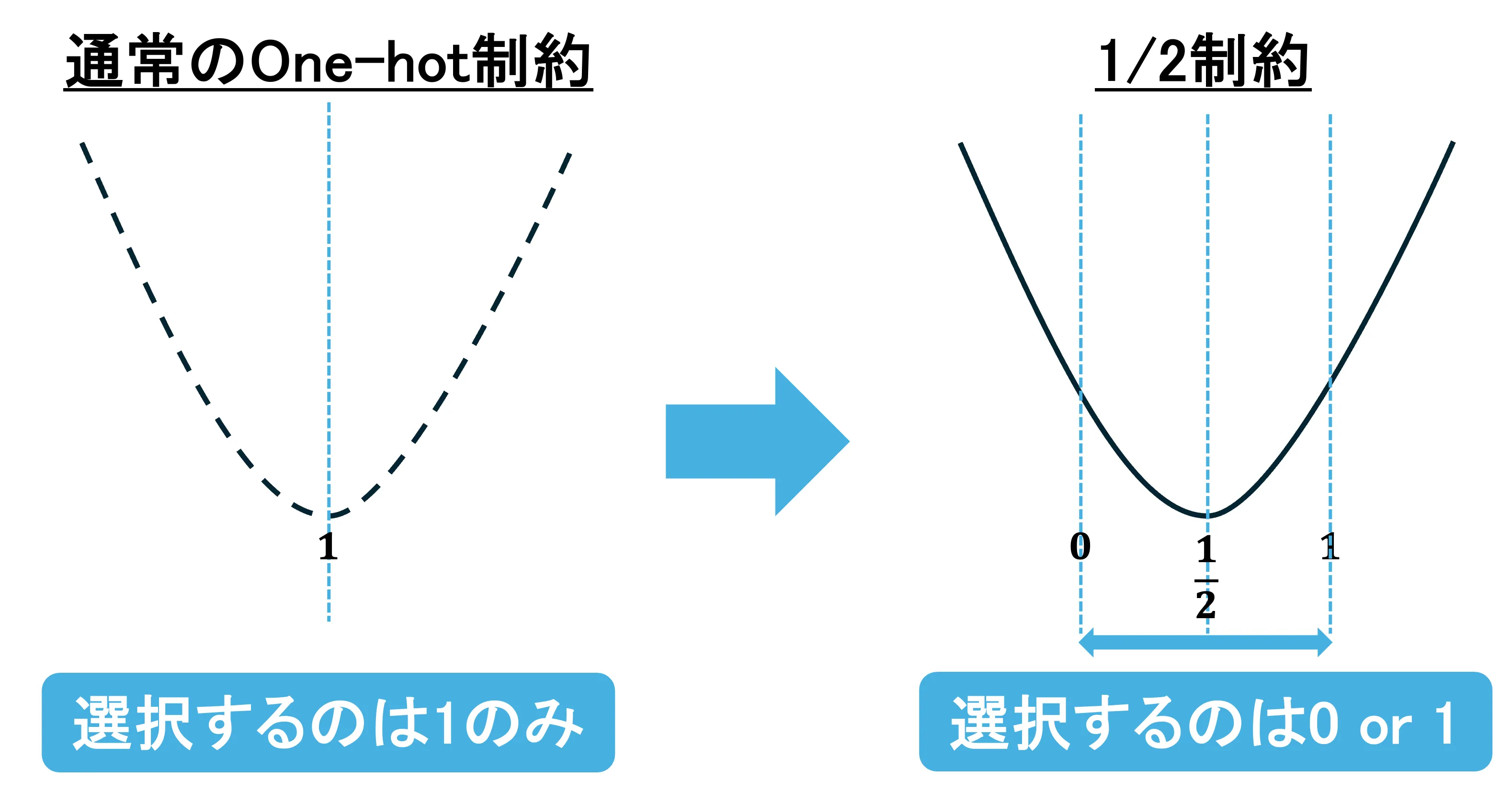
1/2制約は、one-hot制約の応用として用いられる手法です。

通常のone-hot制約は、最小値として$1$になる部分を選択しますが、1/2制約では、$1/2$になる部分を最小値として選択することで、0 or 1の選択をすることができます。

つまり、「必ず1つのタスクを割り当てる」 or 「タスクを割り当てない」ということを柔軟に選択させることができます。

第5項について

対象とするスケジューリング問題に事前に定められている変数

$$D_{f,t} = \begin{cases} 1 ：& \text{タスク $f$ を時間の最小単位 $t$ に割り当て可能}, \\ 0 ：& \text{それ以外} \end{cases}$$

を利用して、割り当ててはいけない期間にタスクを割り当てないようにする制約項です。

$$E_4 = \sum_{f}\sum_{t}\sum_{p} (1 - D_{f,t})\, x_{p,f,t}.$$

この項は、$D_{f,t}=0$のとき、すなわち割り当ててはいけない期間にタスクを割り当てた場合にペナルティが発生するように設計しています。

下記の表1は、$x_{p,f,t}$と$D_{f,t}$の組み合わせごとに、ペナルティの和の中身がどのようになるかを示したものです。

表 1：$x_{p,f,t}$と$D_{f,t}$の組み合わせ

$x_{p,f,t}$（仕事を担当するかどうか）	$D_{f,t}$（タスク割り当て可能かどうか）	罰金の値
0	0	0
1	0	1
0	1	0
1	1	0

$D_{f,t}=0$ 、すなわち割り当ててはいけない期間の場合には、$x_{p,f,t}=1$とした場合にペナルティが発生します。

$D_{f,t}=1$ 、すなわち割り当てが可能な期間の場合には、この項からはペナルティが発生しないため、他の項の制約条件に従って割り当てが行われます。

第6項について

第6項は複数のプロジェクトが存在した際に、各プロジェクト内で決められているタスクの処理順番を決められた順番通りに実行するように割り当てを行う制約項です。

$$E_5 = \sum_{(i \prec j)} \sum_{t} \left(\sum_{p} x_{p,j,t}\right) \left(\sum_{p'} \sum_{t' \ge t} x_{p',i,t'}\right).$$

まずは簡単な意味を捉えましょう。 ここで、$(i \prec j)$はタスク$i$がタスク$j$よりも前に実行されなければならないことを意味しています。 和の中身は、

• 時刻$t$にタスク$j$を実行している作業者の人数

  $$\sum_{p} x_{p,j,t}$$

• 時刻$t$以降にタスク$i$を実行している作業者の人数

  $$\sum_{p'} \sum_{t' \ge t} x_{p',i,t'}$$

の積になっており、タスク$j$よりも早く終わらせるべきであるタスク$i$がタスク$j$よりも後ろにあると、$(\sum_{p} x_{p,j,t})(\sum_{p'} \sum_{t' \ge t} x_{p',i,t'})$分だけペナルティが発生します。

量子アニーリングでは、エネルギーを最小化するような解を探してくるので、エネルギーが高くなるような選択肢は選ばないということを逆手に取った項の設計になっています。

まとめると、タスク$j$が時刻$t$に存在する（始まっている）条件

$$\sum_{p} x_{p,j,t}>0$$

が満たされている際には、タスク$i$が時刻$t$以降に存在しない条件

$$\qty(\sum_{p} x_{p,j,t})\qty(\sum_{p'} \sum_{t' \ge t} x_{p',i ,t'})=0$$

を満たしてほしいという意味になります。

---

3. 実験

ここでは、量子アニーリングを用いて、提案したQUBO式によって実行可能解が得られるかどうかを見ていきましょう。

提案するQUBO式を量子アニーリングを使用して下記の問題サイズで実装してみます。 なお、本問題は全結合の問題であり、変数の数は$\text{worker} \times \text{task} \times \text{time}$だけかかるので、本問題サイズの場合、$3 \times 5 \times 190$となります。

ここで実施期間は19日としていますが、作業者ごとの工数変化に対応するため1日を$dt$分割した時間枠に割り当てを行っており、$\text{time}=190$となります。

したがって、3人の作業員が5つのタスクを19日の期間以内に行う場合、$2850(=3 \times 5 \times 190)$変数を使用すると推測できます。

これは量子アニーリングが解くことのできると言われている180変数を大きく超える値であるため、今回はハイブリッドソルバーであるBQMのLeapHybridSamplerを用いた結果を示します。

ノート

2025年12月時点で、量子アニーリングで解くことのできる変数の数は180程度と言われています。

ノート

様々な量子アニーリングソルバー
D-Wave Systems社が提供する量子アニーリングマシンには、使用する用途によっていくつか種類があります。また、大きいサイズを解く際にはハイブリットソルバーという大規模問題用のソルバーが用意されています。しかし、これらのソルバーはマシンタイムを多く使用するため、使用する前にマシンタイム購入者に確認しましょう。

では、今回解く問題設定を明確に定義していきましょう。以下の表2のような問題サイズを考えます。

表 2：検証する問題サイズ

プロジェクト	タスク（プロジェクトにおける処理順番）	作業人数	実施期間
2つ	プロジェクト1：(0→1→2),プロジェクト2：(3→4)	3名	19日

次に、スケジューリング問題への応用（前編）の3.2章で定義した定数の具体的な値を決めていきます。

これは問題設定をする部分なので、自身の設定した問題に必要な値を自身で定義していきましょう。

今回は、例として各タスクの工数と実施時期を以下の表3のように定義しました。

表 3：タスクと工数の関係と実施希望時期

タスク番号	$A_f$（工数：人月）	$D_{f,t}$
タスク 0	0.28	50
タスク 1	0.37	100
タスク 2	0.34	150
タスク 3	0.30	190
タスク 4	0.29	190

表3より、タスク0を終了するには0.28人月必要なことがわかります。

また、$D_{f,t}$は割り当て可能な期間を表しており、表3の数字はスケジューリング期間のはじめから数えて、何個分の時間単位以内で割り当て可能かを示しています。

例えばタスク0の$D_{f,t}=50$は、初日から 50 時間単位分以内に割り当てることができます。すなわち 5 日目まで（1 週間）に割り当て可能であることを意味しています。（ここでは1週間を平日5日間、月20日作業可能であるとしています。）

次に、作業者のスキルレベルによる工数の変化に対応するために、以下の表4のように各スキルレベルに対して、実質行った作業倍率を定義します。

表 4：スキルレベル別作業工数倍率

スキルレベル	工数倍率
レベル 1	0.50
レベル 2	0.71
レベル 3	1.00
レベル 4	1.25
レベル 5	1.42

これは実際に割り当てられた工数に、それぞれ作業者のスキルレベルをかけることで実質行った仕事量として換算しています。

例えば、レベル3の作業者があるタスクを行った場合、その作業量に1をかけます。一方で、レベル1の作業者が行った場合には、その作業量に0.5をかけます。すなわち、レベル1の作業者がそのタスクを行ったとしても、実質行った作業量は半分であるということを表しています。

表4の定義を使って、それぞれの作業者がタスクに対してどのスキルレベルを持つのかを以下の表5のように定義してあげます。

表 5：各作業者と工数倍率の関係 $d_{p,f}$

	Task 0	Task 1	Task 2	Task 3	Task 4
Worker 0	0.50	0.71	0.50	1.25	0.50
Worker 1	0.50	0.50	1.25	0.71	0.71
Worker 2	1.42	0.71	0.50	0.71	0.50

$d_{p,f}$は、スキルレベル表における実質倍率をどの作業者が割り当てられているかを表しています。

例えば、Worker0 はタスク0 に対してスキルレベル 1 ということがわかります。

ここまでで、式を作るための変数の設定と具体的な定数の値の定義が完了しました。では、実際に量子アニーリングに結果を出してもらいましょう。

3.1 結果

今回は定式化のパラメータ$\alpha,\lambda_1,\lambda_2,\lambda_3,\lambda_4,\lambda_5$をそれぞれ$2.0, 100.0, 131.0, 150.0, 50.0, 500.0$に設定して解いた結果を以下に示します。

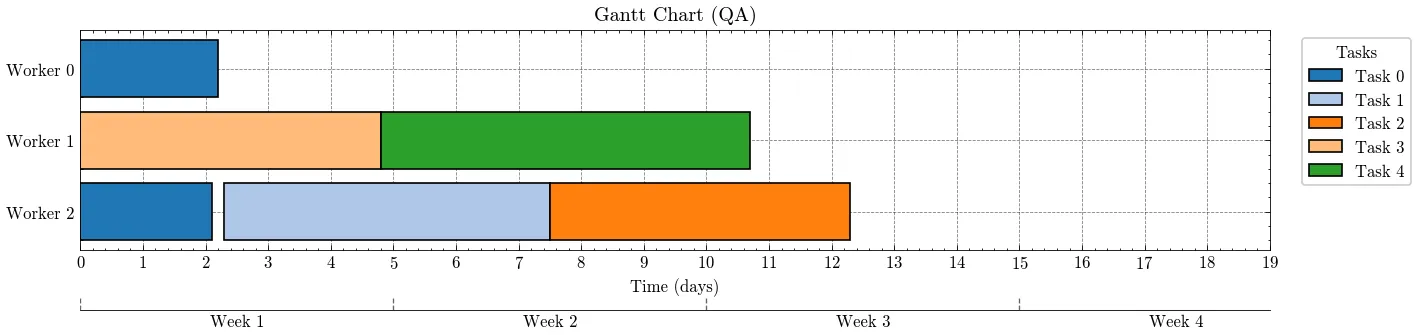
量子アニーリングのハイブリットソルバーを用いて本問題を解いた結果（図1）を見ると、スケジュールの実施期間は19日間と設定しましたが、メイクスパンの最小化によって12日程度で完了できることがわかります。（第1項の効果）

また、プロジェクト内の順番タスク0→タスク1→タスク2、タスク3→タスク4を守って割り当てがされていることや、割り当てバーが重複していないことから提案したQUBOが目的関数と制約を考慮しながら、割り当てを行うことができています。（それぞれ第6項、第4項の効果）

さらに、タスク0は1週目（5日以内）に、タスク1は2週目以内に完了しているなど、割り当ててほしい期間にタスクが行われていることがわかります。（第5項の効果）

図 1：量子アニーリングによるガントチャートの結果

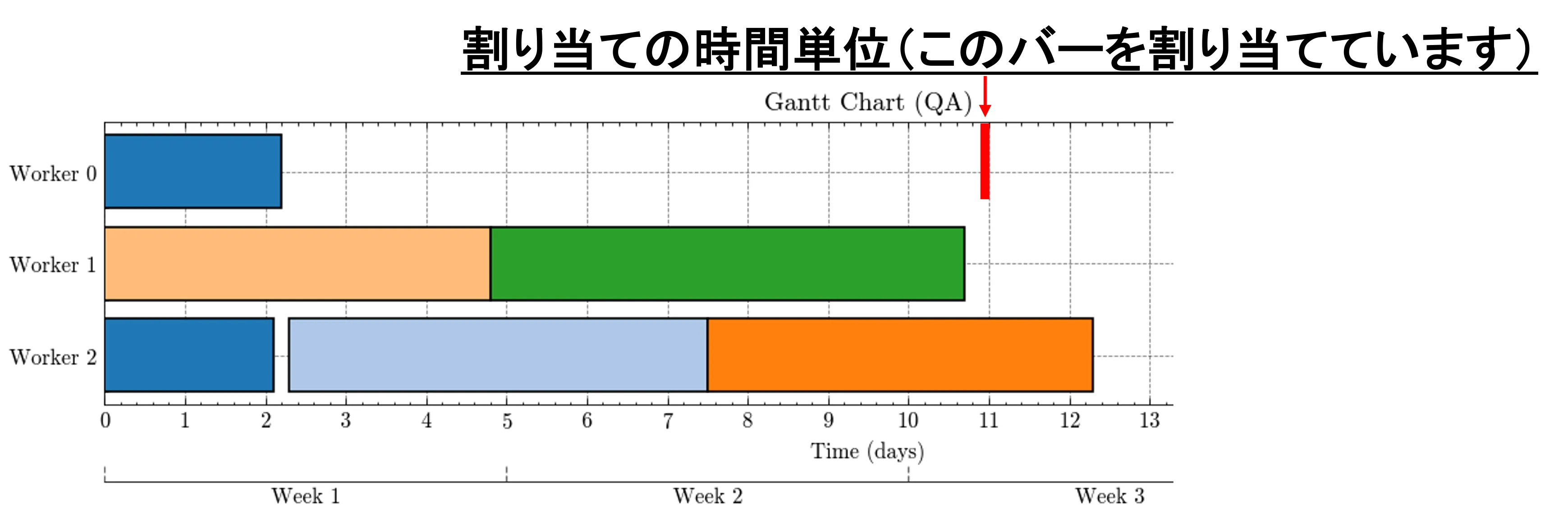
なお、わかりにくいのですが、割り当てを行っている最小単位時間は、図2の赤線の単位ごとです。図2を見ると、同じタスクは時間を空けずに割り当てられていることがわかります。よって、タスクをなるべく連続で割り当てることができています。（第3項の効果）

図 2：ガントチャートの割り当て最小単位

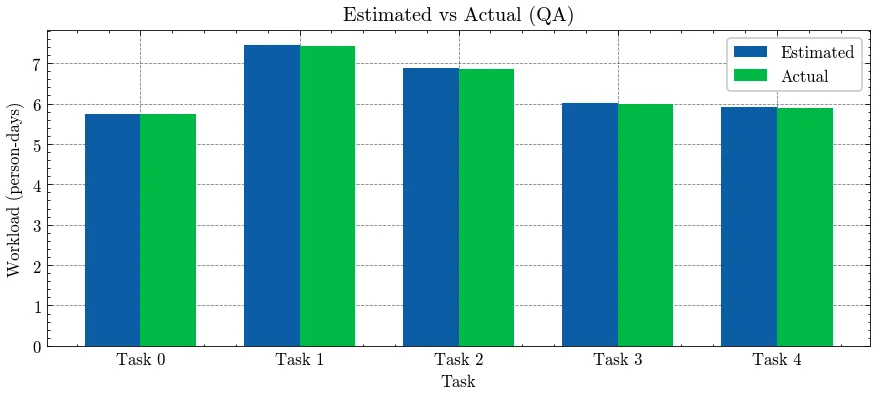
さらに図3からわかる通り、各タスクの工数を満たして割り当てを行うことができています。（第2項の効果）

図 3：割り当てタスク量と必要タスク量の比較

この結果から、今回の問題設定では量子アニーリングを用いて実行可能解が得られていることがわかります。

なおこの結果は、厳密解ソルバーであるGurobiの出した解と近く、ある程度最適解に近い解を出せていることがわかっています。

---

4. まとめ

このページでは、ソフトウェア産業や製造業で重要となるスケジューリング最適化について、定式化の考え方を詳しく解説し、実際に数式として問題を組み立てることで最適化結果が得られるまでの流れを紹介しました。

QUBO形式で問題を定式化する際には、自分が解こうとしている問題をどのように数学的に表現するかがとても重要です。今回扱った例は、やや複雑で難易度の高い内容ではありますが、最適化の本質を学ぶ良い題材になっています。

まずは、もっとシンプルなスケジューリング問題や身近な例を使って、文章を数式に落とし込む練習 を積み重ねてみてください。 その経験が、さまざまな問題を自分で最適化できる力へとつながっていくはずです。

なお、この研究は現在論文執筆中の内容になります。

また、内容は変更される場合があります。

---

5. 本セクションの担当者

東北大学 情報科学研究科 大関研究室 修士2年

矢代開士