スケジューリング問題への応用（前編）

ノート

最適化問題の応用例として、スケジューリング問題の紹介をします。

1. 背景

1.1 人員スケジューリング問題とは？

作業者や仕事、スケジュール（実施時間）がある際に、どの作業者をどの仕事にいつ割り当てるのかを決定する問題のことを言います。

実応用では、工場ラインの人員配置、コールセンターのシフト作成、病院や介護施設の勤務割り当て、さらには物流倉庫での作業ローテーション管理など、限られた人員を効率よく配置するために広く利用されています。これによって、生産性の向上や負担の平準化、人件費の最適化を実現することができます。

難しい点

人員スケジューリング問題の難しい点として、以下がよく挙げられます。

• 作業者数や仕事の数が多くなると、割り当てを行うこと自体が困難になる。
• 問題サイズが大規模化すると割り当てにかかる時間が膨大になる。
• 制約条件が多くなりがちで、厳密解を求めることが困難になる。

目的関数としてよく設定される事項

スケジューリング問題において、目的とされる課題には以下があります。

• 従業員数の削減
• 仕事量の等価配分
• Makespan（作業スケジュール全体の期間）の最小化

今回は、表1のような要員割り当てイメージのように、各タスクの工数や作業順番等を考慮し、全体スケジュールが最も早く終わる要員配置を求めたいとします。

この表1はガントチャートと呼ばれ、主にソフトウェア産業におけるソフトウェア設計、製造業における作業の流れや担当者を管理するためによく用いられています。

表 1：要員割り当てイメージ

プロジェクト名	作業	工数	8月1週目	8月2週目	8月3週目	8月4週目
プロジェクトA	タスク1	0.1	作業者A
プロジェクトA	タスク2	0.2	作業者A
プロジェクトA	タスク3	0.25		作業者A
プロジェクトA	タスク4	0.5			作業者A	作業者A
プロジェクトB	タスク1	0.25	作業者B
プロジェクトB	タスク2	0.1		作業者B
プロジェクトB	タスク3	0.15		作業者B

1.2 工数とは？

工数とは、作業を完了するために必要な作業者数と期間で作業量を表したものです。人時、人日、人月など時間の単位によってそれぞれ定義されており、プロジェクト管理においては人月がよく使われます。

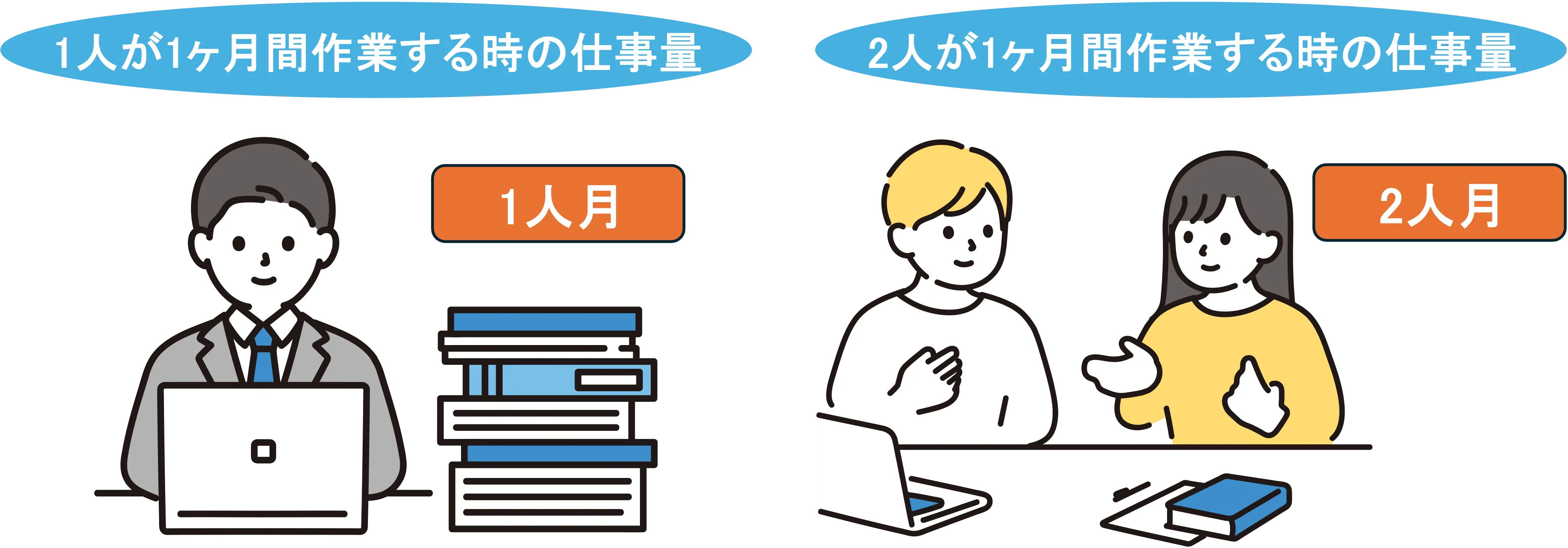1人月（にんげつ）とは、1人が1ヶ月間作業した場合の作業量のことを指します。

つまり、 $\text{人月}=\text{人数} \times \text{月数}$ となります。

プロジェクト管理において作業の見積もりを出す方法としてよく使用される指標です。

---

2. 最適化の条件について

今回は以下の条件を考慮することを目標としてQUBO形式で定式化を行います。

1. Makespanの最小化（全体スケジュールを早く終わらせる）
2. 作業者毎のタスクの工数変化を考慮する
3. 作業者毎の割り当て可能タスクを考慮する
4. タスクごとの希望実施時期を考慮する
5. 同一プロジェクトで作業順番を守る

以上に加えて、ガントチャート（作業工程表）を作る上で必要になる条件があります。

1. 割り当てられたタスクの連続性を考慮しなければならない
2. 作業者に一度に割り当てるタスク量が多すぎてはならない

2.1 本定式化における工夫点

人員スケジューリング問題をQUBO定式化で解いた例はすでにいくつか存在しています。

今回のQUBO定式化において注目してほしい部分として以下が挙げられます。

• 作業者によって担当するタスクのスキルレベルが異なること
• タスクごとに実施してほしい時期が決まっていること
• プロジェクトの中で、タスクを行う順番がすでに決まっていること

3. 定式化

ここでは、前章の条件を数式で表現する（定式化する）方法について示します。

このスケジューリング問題では、例えば以下のように定式化することができます。

$$E = \alpha E_\alpha + \lambda_1 E_1 + \lambda_2 E_2 + \lambda_3 E_3 + \lambda_4 E_4 + \lambda_5 E_5$$

なお、$\alpha$と$\lambda(i=1,2,3,4,5)$はそれぞれ各項の重みを表現しています。また、$E_i(i=\alpha ,1,2,3,4,5)$はそれぞれ以下のような式になります。

第1項はMakespan（スケジューリング全体の期間）の最小化をするための目的項です。

$$E_\alpha = \sum_{p} \sum_{f} \sum_{t} t\, x_{p,f,t}$$

第2項は各作業者の作業工数の変化を考慮しながら、実際に割り当てたタスクが見積もり工数を満たすように制約を設ける項です。

$$E_1 = \sum_{f} \qty( \sum_{p} \sum_{t} d_{p,f}\, x_{p,f,t} - \frac{20}{d_{t}} A_{f} )^{2}$$

第3項は割り当てるタスクの連続性を保証するために設計した制約項です。

$$E_2 = \sum_{p} \sum_{f} \sum_{t} \qty( x_{p,f,t} - x_{p,f,(t+1)} )^{2}$$

第4項は同時刻に複数のタスクを割り当てることを禁止する制約項です。

$$E_3 = \sum_{p} \sum_{t} \qty( \sum_{f} x_{p,f,t} - \frac{1}{2} )^{2}$$

第5項は割り当ててはいけない期間にタスクを割り当てないようにする制約項です。

$$E_4 = \sum_{f} \sum_{t} \sum_{p} (1 - D_{f,t})\, x_{p,f,t}$$

第6項は複数のプロジェクトが存在した際に、各プロジェクト内で決められているタスクの処理順番を決められた順番通りに実行するように割り当てを行う制約項です。

$$E_5 = \sum_{(i \prec j)} \sum_{t} \qty( \sum_{p} x_{p,j,t} ) \qty( \sum_{p'} \sum_{t' \ge t} x_{p',i, t'} )$$

それぞれの項の詳しい内容や意味はスケジューリング問題への応用（後編）で解説しています。

ノート

こちらはあくまで一例ですので、ご自身で設計した決定変数$x$と定式化をぜひ考えてみてください。

ヒント

あまり項を増やしすぎないことがポイントです。

3.1 決定変数の設定

ここでは、定式化の第一歩である決定変数の設定について説明します。

今回の問題に対しては、決定変数として$x_{p,f,t}$を以下のように定義します。

$$x_{p,f,t} = \begin{cases} 1 ：& \text{作業者 $p$ がタスク $f$ を日付の最小単位 $t$ に担当する}, \\ 0 ：& \text{それ以外}. \end{cases}$$

ヒント

決定変数の添え字を増やすことで、決定変数$x$が持つ意味の解釈を広げることができます。

ノート

ただし、最適化結果の解釈の仕方が難しくなったり、使用する量子ビットの数が多くなり、大規模な問題を表現するための量子ビットが足りなくなったりすることもあるので注意が必要です。

3.2 定数の設定

ここでは、定式化に使用する定数の定義をします。

自身で設定した問題に対する定数の意味を考えることも重要な過程になります。

今回は定式化に必要な定数の定義として以下の表2のように設定します。

表 2：定数の定義

変数	意味	取りうる値
$d_t$	日メモリの幅 （今回の実験では0.1に固定します）	実数
$d_{p,f}$	作業者$p$がタスク$f$を担当したときの実質作業倍率	実数
$A_f$	タスク$f$の見積もり工数（人月）	実数
$D_{f,t}$	週$t$にタスク$f$を行う予定になっているかどうか	0 (なし) or 1 (あり)

今回は、7.5時間/1日として作業を行うとします。

ここで、日メモリの幅とは何時間単位でタスクを割り当てるかということを表しています。よって、$d_t=0.1$とは、1日を10分割した時間単位（0.75時間単位または45分単位）で割り当てるということを意味しています。

3.3 ハイパーパラメータの設定

ここでは、各項の強さを調整するハイパーパラメータ（重み）の定義をします。

• $\alpha \in \mathbb{R}$（実数）：目的項の重み
• $\lambda_1,\lambda_2,\lambda_3,\lambda_4,\lambda_5\in \mathbb{R}$（実数）：QUBO定式化の各項（制約条件）における重み

ヒント

このハイパーパラメータの調整が大事になります。 各項のオーダーの調整を行うことにより、ハイパーパラメータが決定しやすくなります。 項が増えると調整が難しくなるので、定式化は単純化を意識しましょう。

---

4. まとめ

このページでは、ソフトウェア開発や製造業の現場でよく使われるガントチャートを例に、人員スケジューリングをどのように「最適化問題」として扱うのか、その考え方から数式として表現するまでの流れを紹介しました。

最適化問題を数式で表す際に重要になるのが、どの値を固定された定数として扱うか、そして、どの値を解くべき変数（決定変数）として設定するかという点です。これらの設定は、問題を正しく解くための土台となる非常に大切なステップです。

最適化の立式には、他にもさまざまな方法や表現があります。本ページの内容だけでなく、参考文献や他の記事もあわせて確認しながら、扱いたい実際の問題に合う形で最適な問題設定を行ってみてください。

今回紹介した定式化の詳細や、実際に設定した定数の具体的な値、また最適化によってどのようなスケジューリング結果が得られたのかについては、続編であるスケジューリング問題への応用（後編）で詳しく解説しています。 より踏み込んだ内容に興味のある方は、ぜひそちらもあわせてご覧ください。

なお、この研究は現在論文執筆中の内容になります。

また、内容は変更される場合があります。

---

5. 参考文献

• Serap Ulusam Seçkiner and Mustafa Kurt. “A simulated annealing approach to the solution of job rotation scheduling problems,” Applied Mathematics and Computation 188.1 (2007), 31-45
• Tadashi Kadowaki and Hidetoshi Nishimori, “Quantum annealing in the transverse Ising model,” Physical Review E 58.5 (1998), 5355

---

6. 本セクションの担当者

東北大学 情報科学研究科 大関研究室 修士2年

矢代開士