組合せ最適化によるレコメンド

ノート

最適化問題の応用例として、レコメンドタスクを紹介をします。

レコメンドタスクとは

膨大なアイテム集合(商品、コンテンツ、人材など)の中から、ユーザが関心を持ちそうなアイテムやコンテンツを数個選んで提示するタスクです。 ECサイト、動画配信、SNS、広告配信など、現代のあらゆるデジタルサービスにおいて、ユーザと情報の最適なマッチングを実現するレコメンドシステムは、ユーザ体験（UX）とビジネスの収益を支える最も重要なインフラとして、極めて高い需要があります。

1. 背景

現代のレコメンドタスクにおいて、ユーザの好みを高精度に予測する技術はすでに成熟しつつある一方、実際のビジネスやサービス運用においては、単に「予測スコアが高い順」にアイテムを並べるだけ（ランキング形式）では、不十分なケースが多々あります。

なぜなら、優れたレコメンドリストを作成するには、個々のスコアだけでなく、リスト全体としてのバランスや制約を考慮する必要があるからです。それらの例として、以下が挙げられます。

• 多様性 ：似たようなアイテムばかりを並べないこと

• 予算制約：合計金額やリソースの上限（予算内）や、「ちょうど使い切る」などの条件を守ること

• 併売効果：一緒に選ぶことで価値の上がる組み合わせを提案すること

今回はレコメンドタスクを 制約なし二値二次計画問題(QUBO) で定式化し、量子アニーリングやシミュレーテッドアニーリングを使って解くことで、アイテム間の多様性、予算制約、併売効果といった複雑な条件を考慮したレコメンドによるユーザ体験の最大化を目指します。

2. 問題設定

数式による定式化を行う前に、レコメンドタスクを具体的なショッピングのシナリオで考えてみましょう。 ここでは、 「ECサイトなどで様々なカテゴリが混在するアイテムの候補リストから、予算内で全身のコーディネイトを成立させる」 という問題を考えます。

今回、アイテムはID、カテゴリ、商品名、価格、そしてユーザがそのアイテムをどれくらい好むかを表す 「スコア（予測評価値）」 を持つ、合計8個のデータセットを使用します。

候補アイテムリスト

ID	カテゴリ	商品名	スコア	価格
1	トップス	ロゴTシャツ	90点	4,000円
2	トップス	白シャツ	70点	5,000円
3	ボトムス	デニムパンツ	80点	10,000円
4	ボトムス	スラックス	60点	8,000円
5	シューズ	スニーカー	75点	8,000円
6	アウター	ジャケット	95点	20,000円
7	小物	キャップ(帽子)	88点	3,000円
8	小物	トートバッグ	85点	4,000円

このとき、レコメンドとは、アイテムの中からスコアの合計がもっとも高い組み合わせを探すことです。

ただし、スコアだけでなく幾つかの条件を同時に考慮する必要があります。 まず、全身コーデを成立させるために、「トップス」、「ボトムス」、「シューズ」 の3カテゴリは必須であり、各カテゴリから1個ずつ選ぶ必要があります。 逆に、「アウター」、「小物」 は任意カテゴリとして、カテゴリごとに0個または1個まで選べるとします。 また、予算は25,000円とし、合計金額が25,000円に近い程よいレコメンドとします。

まとめると、今回のレコメンドタスクは以下の条件を満たす組み合わせを探すことになります。

2.1 レコメンドの条件

1. 必須カテゴリ: 「トップス」、「ボトムス」、「シューズ」をそれぞれ1個ずつ含む
2. 任意カテゴリ: 「アウター」、「小物」は、カテゴリごとに0個または1個まで選べる（選ばなくてもよい）
3. 合計金額: 合計金額は25,000円に近い程よい
4. 合計スコア: 合計スコアは高い程よい

ヒント

今回は上記をレコメンドの条件としていますが、これはあくまで一例ですので、自分の実現したいレコメンドに応じて設定することもできます。

ノート

このレコメンドの条件を元に定式化を行うので、各条件はシンプルにしておくと後の定式化がしやすくなります。

2.2 本問題設定の最適解

今回の最適解は、次で与えられます。

ID	カテゴリ	商品名	スコア	価格
1	トップス	ロゴTシャツ	90点	4,000円
3	ボトムス	デニムパンツ	80点	10,000円
5	シューズ	スニーカー	75点	8,000円
7	小物	キャップ	88点	3,000円

合計金額: 25,000円 合計スコア: 333点 (90 + 80 + 75 + 88)

従って、我々の目標はこの最適解を見つけることができるレコメンドシステムを構築することです。

3. 貪欲的なレコメンド

まず、非常に単純なレコメンドシステムを考えてみましょう。 アイテムをスコアの高い順に並び替え、予算内で上から順にアイテムを選んでいく貪欲法(Greedy Method) によるレコメンドを行ってみます。

候補アイテムリストをスコア順に並び替えると、次のようになります。

候補アイテムリスト(スコア順)

順位	ID	カテゴリ	商品名	スコア	価格	累積金額
1	6	アウター	ジャケット	95点	20,000円	20,000円
2	1	トップス	ロゴTシャツ	90点	4,000円	24,000円
3	7	小物	キャップ(帽子)	88点	3,000円	27,000円
4	8	小物	トートバッグ	85点	4,000円	31,000円
5	3	ボトムス	デニムパンツ	80点	10,000円	41,000円
6	5	シューズ	スニーカー	75点	8,000円	49,000円
7	2	トップス	白シャツ	70点	5,000円	54,000円
8	4	ボトムス	スラックス	60点	8,000円	62,000円

貪欲法に従うと、まず、スコアが最も高い「ジャケット（20,000円）」が選ばれます。 次に、2番目にスコアの高い「ロゴTシャツ（4,000円）」が選ばれます。 その後、3番目にスコアの高い「キャップ（3,000円）」を選ぼうとすると、予算オーバーとなるため選択が終了します。 結果として、貪欲法は「ジャケット」「ロゴTシャツ」の2点（合計24,000円）という組み合わせをレコメンドします。

しかし、必須カテゴリである「ボトムス」や「シューズ」がレコメンドされておらず、 「全身コーデを成立させる」 という条件を満たすことができませんでした。

このように、個々のスコアだけを見て判断した組み合わせ（局所最適解）では、全体のバランスやルールを守った最適な組み合わせ（大域最適解）にたどり着けないことがあります。

4. QUBO最適化によるレコメンド

よりよいレコメンドシステムとして、QUBO最適化によるレコメンドを導入します。 すなわち、今回のレコメンドの条件をQUBO(制約なし二値二次計画問題)に定式化し、これを解くことで最適なアイテムの組み合わせを得ることを目標にします。

4.1 変数の定義

今回、最適化対象はアイテムの組み合わせなので、変数はアイテムの添字$k$を導入して、次式で定義します。

$$x_k = \begin{cases} 1 & \text{アイテム$k$をレコメンドする} \\ 0 & \text{アイテム$k$をレコメンドしない} \end{cases}$$

ここで、$k \in \{1, 2, 3, 4, 5, 6, 7, 8\}$は各アイテムのIDを表します。

具体例：

• $x_1 = 1$：ロゴTシャツをレコメンドする
• $x_1 = 0$：ロゴTシャツをレコメンドしない
• $x_6 = 1$：ジャケットをレコメンドする
• $x_6 = 0$：ジャケットをレコメンドしない

従って、あらゆるアイテムの組み合わせは$(x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8)$ のように表されます。

4.2 定数の定義

次に、各アイテムの価格、カテゴリ、スコアなどの定数も文字を使って定義しておきましょう。

$b_{k}\in \mathbb{N}$：アイテム$k$の価格

$s_{k}\in \mathbb{N}$：アイテム$k$のスコア

$c_{k,m}$：アイテム$k$がカテゴリ$m$に属するかどうかのフラグ

$$c_{k,m}= \begin{cases} 1 & \text{アイテム$k$がカテゴリ$m$を持つ} \\ 0 & \text{アイテム$k$がカテゴリ$m$を持たない} \end{cases}$$

また、以降の制約を簡潔に書くためにカテゴリ集合を導入します。
必須カテゴリを $M_\text{req}$、任意カテゴリを $M_\text{opt}$ とし、ここでは次のように定めます。

$M_\text{req}=\{\text{トップス},\text{ボトムス},\text{シューズ}\}$

$M_\text{opt}=\{\text{アウター},\text{小物}\}$

ヒント

各アイテムがどのカテゴリに所属するかといった属性情報は、グループ添字を導入することで表現できます。

4.3 定式化

ではここから、定義した変数、定数を使って定式化に入っていきます。

本問題を定式化する前に、レコメンドで満たすべき条件を再掲します。

1. 必須カテゴリ: 「トップス」、「ボトムス」、「シューズ」はそれぞれ必ず一つ選ぶ
2. 任意カテゴリ: アウター、小物などの任意カテゴリのアイテムは、カテゴリごとに0個または1個まで選べる（選ばなくてもよい）
3. 予算: 合計金額をちょうど25,000円にする
4. 合計スコア最大化: できるだけ合計スコアを高くする

では、これらの制約をQUBOに落とし込んでいきましょう。

ヒント

各条件を定式化していくにあたって重要なことは、条件が満たされるときに値が小さくなるようにQUBOを設計することです。

条件1（必須カテゴリ制約）

「トップス」「ボトムス」「シューズ」などの必須カテゴリ（集合$M_\text{req}$）については、選んだ個数の合計が「1」になることを目指します。

まず、あるカテゴリ$m\in M_\text{req}$に属するアイテムの選択数の合計は次式で表されます:

$$\sum_{k}c_{k,m}x_k$$

ある必須カテゴリ$m$において、選んだアイテムの個数の合計が1になるとは、この値が1になることを意味します。 ゆえに、我々が目指す定式化は、次の値の最小値が0になるようにすることです:

$$\sum_{k}c_{k,m}x_k - 1$$

それを満たす関数は2次関数であり、単に上式を2乗することで表されます:

$$\left(\sum_{k}c_{k,m}x_k - 1\right)^2$$

これは、ある1つの必須カテゴリ$m$に対する式であったので、これらをすべての必須カテゴリに対し足し合わせたものが、条件1のQUBO表現$H_1$となります:

$$H_1=\sum_{m\in M_\text{req}}\left(\sum_{k}c_{k,m}x_k-1\right)^2$$

• 1個選んだ場合：$(1-1)^2 = 0$ （ペナルティなし）
• 選ばない場合：値が大きくなりペナルティとなる

条件2（任意カテゴリ制約）

必須以外のカテゴリ（集合$M_\text{opt}$）については、「0個」または「1個」のどちらかであればOKとし、「2個以上」選ぶことを禁止します。これを実現するために、ターゲットを $0$ と $1$ の間である $0.5$ に設定します。

$$H_2=\sum_{l\in M_\text{opt}} \left(\sum_{k}c_{k,l}x_{k}-1/2\right)^2$$

条件3（予算制約）

今回は予算を余らせず、合計金額がちょうど25,000円にする組み合わせを探します。

$$H_3=\left(\sum_{k}b_kx_k-25000\right)^2$$

ノート

価格は桁が大きいため、そのままでは二乗誤差項が過大になり、他の項の影響を打ち消してしまう恐れがあります。 これを防ぐため、価格 $b_k$ と目標金額（25,000円） の双方を同じ係数（例：価格の最大値）で割り、0〜1程度の範囲に規格化して扱うのが一般的です。

※今回は簡単のためそのまま記載しています

条件4（合計スコア最大化）

レコメンドしたアイテムのスコア$s_k$の合計ができるだけ大きくなるようにする。 QUBOは最小化問題なので、ここでは合計スコアを最大化する代わりに負号を付けて最小化する。

$$H_{\text{score}}=-\sum_{k}s_kx_k$$

全体の目的関数

これらを重み係数$\lambda_*$を掛けて足し合わせたものが、最終的なQUBOとなります。

$$H=\lambda_1 H_1+\lambda_2 H_2+\lambda_3 H_3+\lambda_4 H_{\text{score}}$$

この $H$ を最小化する $x$ の組み合わせを探索することで、条件を満たす最適なレコメンドリストが得られます。

ノート

この重み係数$\lambda_*$に理論的な絶対の正解はありません。 実務においては、条件を全て満たした解が確実に出力されるように、 実験的に係数を調整（チューニング）して決定します。

4.4 実験結果

では、実際に今回の定式化を実装して、OpenJijのSASamplerで解いた結果を示します。 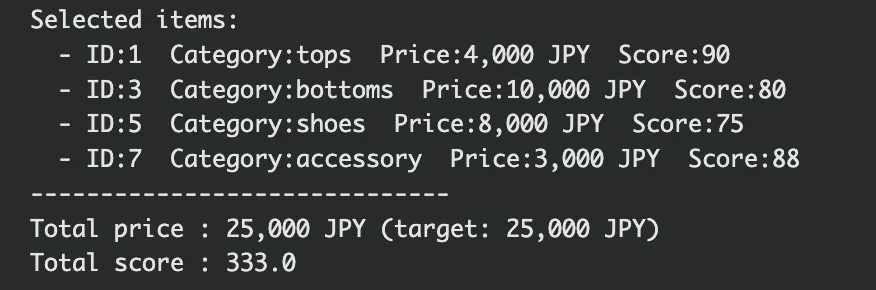上記から、QUBO最適化の結果として次のアイテムが選ばれたことが分かります。

ID	カテゴリ	商品名	スコア	価格
1	トップス	ロゴTシャツ	90点	4,000円
3	ボトムス	デニムパンツ	80点	10,000円
5	シューズ	スニーカー	75点	8,000円
7	小物	キャップ(帽子)	88点	3,000円

よって、今回の問題において、QUBO最適化は設定した条件を満たすレコメンドを実現できたことが確認できました。

5. 本定式化の発展

ここまでの定式化では、個々のアイテムのスコアや価格（1次の項 $x_k$）をメインに扱ってきました。しかし、QUBO（二次計画問題）の最大の強みは、「アイテムAとアイテムBを同時に選んだらどうなるか」 というアイテム間の相互作用(2次の項 $x_k x_{k'}$) を自然にモデルに組み込める点にあります。

ここでは本定式化の拡張例として二つのアイテム間の相互作用を紹介します

5.1 拡張1：相性の良さを考慮する（併売効果）

「ジャケットを買うなら、それに合うスラックスも提案したい」といった、アイテム間の 相性（シナジー） を考慮してみましょう。

事前にアイテム $k$ とアイテム $k'$ の相性スコア $p_{k,{k'}}$ を定義しておきます。これは、値が大きいほど相性が良いことを示します。 このとき、両方のアイテムが選ばれたとき（$x_k=1$ かつ $x_{k'}=1$）に、相性スコア分だけエネルギーを下げる（報酬を与える）項を追加します。

$$H_{\text{synergy}} = - \sum_{k < {k'}} p_{k,{k'}} x_k x_{k'}$$

$x_k, x_{k'}$ が共に1の場合：$-p_{k,{k'}}$ が加算され、エネルギーが下がる（＝より良い解とみなされる）。どちらか一方でも0の場合：項は0になり、影響しない。これにより、単独のスコアがそこそこでも、「組み合わせると最高」なペアが選ばれやすくなります。

5.2 拡張2：多様性の確保（類似度ペナルティ）

今回の問題設定（全身コーデ）とは若干異なりますが、例えば「Tシャツをおすすめする」といった同カテゴリ選出のシナリオでは、アイテム間の多様性 の考慮も必要になってきます。

例えば「Tシャツを提案する際、ブランドが異なる白の無地Tシャツばかり3枚選ばれる」といった事態は避けたいものです。このように、似すぎているアイテム同士が同時に選ばれることを防ぐために、類似度（Similarity） を用いたペナルティを導入します。

アイテム $k$ と $k'$ の類似度を $w_{k,{k'}}\in[0,1]$ と定義する。

• $w_{k,{k'}}\approx 1$：非常に似ている
• $w_{k,{k'}}\approx 0$：ほとんど似ていない

そして、両方が選ばれた場合に類似度に比例したペナルティを加える：

$$H_{\text{div}}=\sum_{k<{k'}} w_{k,{k'}}x_kx_{k'}$$

• 似ているペア（$w_{k,{k'}}$が大）を同時に選ぶほどエネルギーが増え、同時選出が避けられる
• 似ていないペア（$w_{k,{k'}}$が小）はペナルティが小さく、同時に選ばれても問題になりにくい

これにより、同じカテゴリ内で複数アイテムを提示する問題でも類似度が低いアイテムが選ばれるようになり、レコメンドリストの多様性（Diversity） が担保されます。

6. まとめ

本稿では、レコメンドを単なる「スコア順のランキング（貪欲法）」ではなく、QUBOとして数学的に記述する手法について解説しました。

• 定式化のアプローチ ：各アイテムを選ぶ／選ばないを二値変数 $x_k\in \{0,1\}$ で表し、カテゴリ条件・予算条件は 破るほど目的関数が増えるペナルティ項として組み込んだ。これにより「条件を満たしつつスコアが高い組合せ」を 最小化問題として一括で探索できる。

• QUBOの強み：$x_k x_{k'}$ のような二次項を入れられるため、「同時に選ぶと嬉しい（シナジー）」や「同時に選ぶと似すぎて困る（多様性）」といった アイテム間の関係を自然にモデル化でき、ランキングでは扱いにくいリスト全体の質 を最適化できる。

7. 本セクションの担当者

東北大学情報科学研究科　大関研究室　 戸枝泰雅